Пример. 1. Требуется найти минимум функции , где А=1; В=2; С=1,2; D=2

1. Требуется найти минимум функции 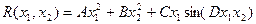, где А=1; В=2; С=1,2; D=2.

2. Интервал поиска: х_1нач = -2, х_1кон = 2, х_2нач = -2, х_2кон = 2.

3. Начальная точка: х₁₀ = 1,4962, х₂₀ = -1.

4. Параметры поиска: шаг h=0,5, погрешность = 0,01.

В окрестности заданной начальной точки (1,4962, -1,0000), R=3,9719 сформируем начальный симплекс, его координатами являются:

№_{вершины}	х₁	х₂	R
	1,7462	-0,8557	4,1938
	1,2462	-0,8557	1,7519
	1,4962	-1,2887	6,7368

Конечно, можно и по-другому построить начальный симплекс, например, заданная начальная точка может являться одной из вершин симплекса, а не лежать внутри симплекса, как в данном случае. Это не принципиально и на результат существенно не влияет.

Не трудно заметить, что самой плохой вершиной является третья (самое большое значение критерия). Удалим эту вершину и на противоположной грани построим новый симплекс. Практически это означает, что нужно найти одну вершину нового симплекса. Применим базовый алгоритм для каждой переменной х₁ и х₂ отдельно.

Получим новую вершину:

№_{вершины}	х₁	х₂	R
	1,4962	-0,4226	0,8839

Теперь симплекс образуют вершины 1, 2, 4. Самая плохая вершина – 4. По аналогичной формуле перейдём к следующей новой вершине, «отразив» удаляемую относительно центра грани.

Получим вершину:

№_{вершины}	х₁	х₂	R
	0,9962	-0,4226	0,4578

Теперь симплекс образуют вершины 2, 4, 5. Самая плохая вершина – 2. Строим следующую вершину:

№_{вершины}	х₁	х₂	R
	1,2462	0,0104	1,5919

Оказалось, что только что полученную вершину нужно будет удалять как самую плохую. Следовательно, необходимо сжимать симплекс, воспользовавшись второй формулой алгоритма.

№_{вершины}	х₁	х₂	R
	1,2462	-0,6392	0,8750

Далее приведём без комментариев координаты вершин следующих симплексов, предоставив учащимся самостоятельно определять самую плохую вершину в каждом текущем симплексе.

№_{вершины}	х₁	х₂	R
	0,7462	-0,6392	0,6435	отражение
	0,4962	-0,4226	0,3610	отражение
	0,7462	-0,2061	0,3707	отражение
	0,2462	-0,2061	0,1157	отражение
…	…	…	…	…
	0,4962	0,0104	0,2526	отражение
	-0,0663	-0,1520	0,0490	сжатие
	-0,3163	0,0645	0,1238	отражение
	0,1056	-0,1385	0,0458	сжатие
…	…	…	…	…
	0,0089	0,0704	0,0100	отражение
	-0,1014	0,0814	0,0256	отражение
	0,0546	0,0199	0,0039	сжатие

Симплекс быстро сжимается вокруг искомой оптимальной точки.

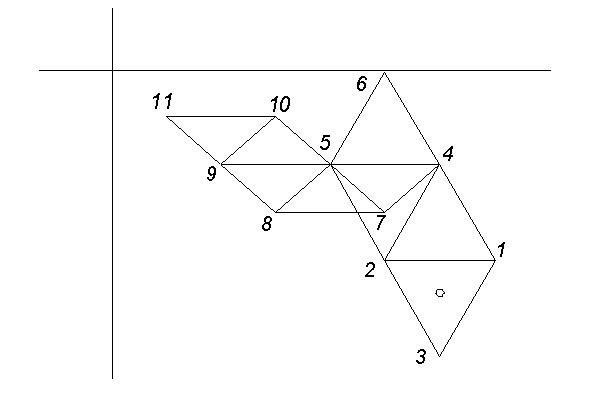
При выходе в район оптимума процесс поиска "зацикливается". Это имеет место тогда, когда приходится выбрасывать только что полученную вершину (эта ситуация возникает в том случае, если значение критерия в новой вершине оказывается самое плохое). В этом случае можно "сжимать" симплекс, откладывая новую вершину от грани на расстоянии вдвое меньше, чем необходимо.

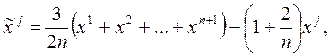
Процесс сжатия происходит многократно, до тех пор, пока размеры симплекса не будут меньше заданных или пока наибольшее расстояние между вершинами симплекса (длина ребра) не будет меньше заданной величины.

Под размерами симплекса понимается расстояние от его центра до всех вершин (в этом случае расстояние от центра до всех вершин должно быть меньше заданного), а иногда и периметр симплекса, т.е. сумма всех его ребер.

Основным недостатком метода является невозможность ускорения поиска вдали от оптимума. Этот недостаток устранен в одной из модификаций метода, известной как метод Нелдера — Мида. В этом варианте симплексного метода предусмотрено растяжение симплекса в случае, если новая вершина лучше лучшей в старом симплексе, а также сжатия симплекса, если новая вершина оказывается хуже наихудшей в старом симплексе.

Имеется также операция уменьшения размера симплекса, называемая редукцией, которая вводится в случае зацикливания. При этом уменьшаются все грани симплекса одновременно в два раза. Уменьшение размера симплекса в два раза осуществляется делением пополам расстояния от каждой точки симплекса до точки х ₁ определяющей наименьшее значение функции, т.е. будет: x_i = x_i^c +0,5(x_i - x ₁).