1. Высказыванием является предложение:
A) 3x + 4y = 1; B) 3x + 4y >1; C) 3 + 4 >1; D) 3 + 4; E) 3x + 4y.
2. Высказыванием является предложение:
A) 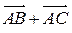 ; B)
; B) 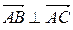 ; C)
; C) 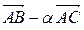 ;
;
D) 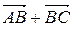 ; E)
; E) 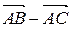 .
.
3. Высказыванием является предложение:
A) 2 + 3; B) 2 + 3 > 4; C) 2 + 3 – 4; D) 2 – 3; E) 3 – 4.
4. Конъюнкцией двух высказываний 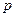 и
и 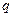 называется …
называется …
5. Дизъюнкцией двух высказываний 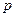 и
и 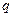 называется …
называется …
6. Эквиваленцией двух высказываний 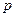 и
и 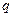 называется …
называется …
7. Следующая таблица истинности определяет логическую операцию над высказываниями:
| A) | А | В | 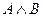 | B) | А | В | 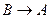 | C) | А | В | 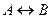 |
| D) | А | В | 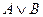 | E) | А | В | 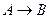 | ||||
8. Следующая таблица истинности определяет логическую операцию над высказываниями:
| A) | А | В | 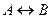 | B) | А | В | 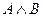 | C) | А | В | 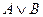 |
| D) | А | В | 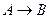 | E) | А | В | 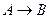 | ||||
9. Следующая таблица истинности определяет операцию над высказываниями:
| A) | А | В | 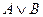 | B) | А | В | 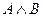 | C) | А | В | 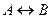 |
| D) | А | В | 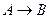 | E) | А | В | 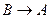 | ||||
10. Полной является следующая система логических операций алгебры высказываний.
A) 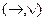 ; B)
; B) 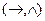 ; C)
; C) 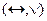 ; D)
; D) 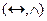 ; E)
; E) 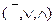 .
.
11. Полной является следующая система логических операций:
A) 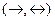 ; B)
; B) 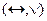 ; C)
; C) 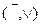 ; D)
; D) 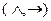 ; E)
; E) 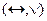 .
.
12. Равносильными являются формулы:
A)  ; B)
; B) 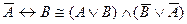 ;
;
C) 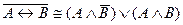 ; D)
; D) 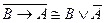 ;
;
E) 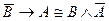 .
.
13. Равносильными являются формулы:
A) 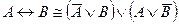 ;
;
B) 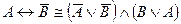 ;
;
C) 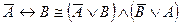 ;
;
D) 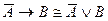 ;
;
E) 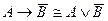 .
.
14. Равносильным и являются формулы:
A) 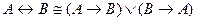 ;
;
B) 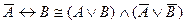 ;
;
C) 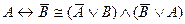 ;
;
D) 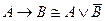 ;
;
E) 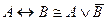 .
.
15. Тавтологией является формула:
C) A 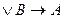 ; B) A
; B) A 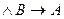 ; C) A
; C) A 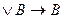 ;
;
D) A 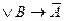 ; E) A
; E) A 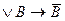 .
.
16. Тавтологией является формула:
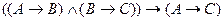 ;
;
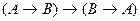 ;
;
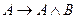 ; D)
; D) 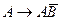 ; E)
; E) 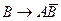 .
.
17. Тавтологией является формула:
A) 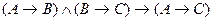 ;
;
B) 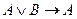 ; C)
; C) 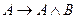 ;
;
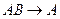 ; E)
; E) 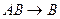 .
.
18. Тавтологией является следующая формула алгебры высказываний.
A) 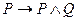 ; B)
; B) 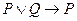 ;
;
C) 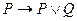 ; D)
; D) 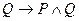 ;
;
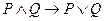 .
.
19. Тавтологией является следующая формула алгебры высказываний:
A) 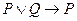 ; B)
; B) 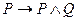 ;
;
C) 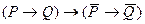 ; D)
; D) 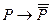 ;
;
E) 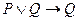 .
.
20. Тавтологией является формула:
A) 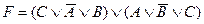 ;
;
B) 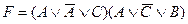 ;
;
C) 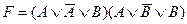 ;
;
D) 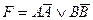 ; C)
; C) 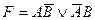 .
.
21. Следующая формула алгебры высказываний является тавтологией:
A) 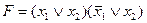 ;
;
B) 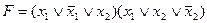 ;
;
C) 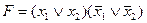 ;
;
D) 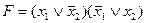 ;
;
E) 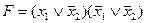 .
.
22. Тавтологией является формула двойственная к формуле F:
A) 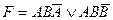 ; B)
; B) 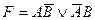 ;
;
C) 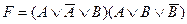 ;
;
D) 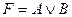 ; E)
; E) 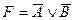 .
.
23. Тождественно – ложной является формула:
A) 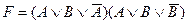 ;
;
B) 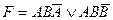 ; C)
; C) 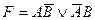 ;
;
D) 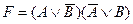 ; E)
; E) 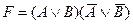 .
.
24. Следующая формула алгебры высказываний является тождественно – ложной:
A) 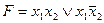 ; B)
; B) 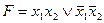 ;
;
C) 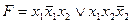 ; D)
; D) 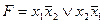 ;
;
E) 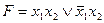 .
.
25. Равносильными являются формулы (где F(x1, x2) - произвольная формула):
A) F*(x1, x2) 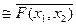 ; B) F*(x1, x2)
; B) F*(x1, x2) 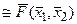 ;
;
D) 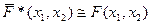 ; D) F*(x1, x2)
; D) F*(x1, x2) 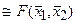 ;
;
E) 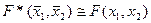 .
.
26. Равносильными являются формулы: (где F(x1,x2,x3) – произвольная формула):
A) 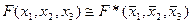 ;
;
B) 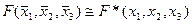 ;
;
C) 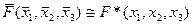 ;
;
D) 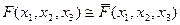 ;
;
E) 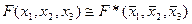 .
.
27. Равносильными являются формулы (где F (x1, x2, x3) – произвольная формула):
A) 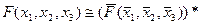 ;
;
B) 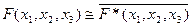 ;
;
C) 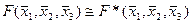 ;
;
D) 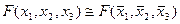 ;
;
E) 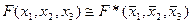 .
.
28. Двойственной к формуле F=(A 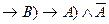 является формула…
является формула…
29. Двойственной к формуле 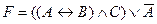 является формула…
является формула…
30. Двойственной к формуле 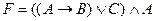 является формула…
является формула…
31. К.Н.Ф. является формула от переменных А, В, С:
A) 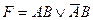 ; B)
; B) 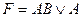 ; C)
; C) 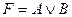 ;
;
D) 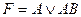 ; E)
; E) 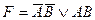 .
.
32. К.Н.Ф. является формула:
A)  ; B)
; B) 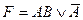 ;
;
C) 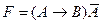 ; D)
; D) 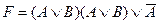 ;
;
E) 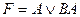 .
.
33. Д.Н.Ф является формула:
A) 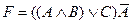 ; B)
; B) 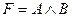 ;
;
C)  ; D)
; D) 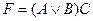 ;
;
E) 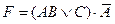 .
.
34. С.К.Н.Ф. является формула от переменных А, В, С:
A) 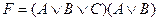 ; B)
; B) 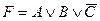 ;
;
E) 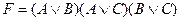 ; D)
; D) 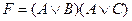 ;
;
E) 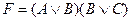 .
.
35. С.Д.Н.Ф. является формула от переменных А,В,С:
A) 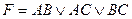 ; B)
; B) 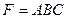 ;
;
C) 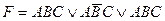 ; D)
; D) 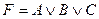 ;
;
E) 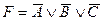 .
.
36. С.Д.Н.Ф является формула от переменных А,В,С:
A) 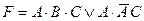 ; B)
; B) 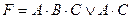 ;
;
C) 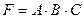 ; D)
; D) 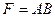 ; E)
; E) 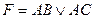 .
.
37. Логическим следствием формул 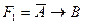 и
и 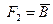 является формула Н:
является формула Н:
A)  ; B)
; B)  ; C)
; C) 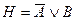 ;
;
D) 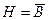 ; E)
; E) 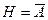 .
.
38. Логическим следствием формул 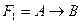 и
и 
 является формула Н:
является формула Н:
A)  ; B)
; B) 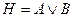 ; C)
; C) 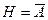 ;
;
D) 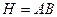 ; E)
; E) 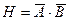 .
.
39. Логическим следствием формул 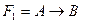 и
и 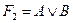 является формула Н:
является формула Н:
A) 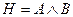 ; B)
; B) 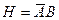 ; C)
; C)  ;
;
D) 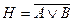 ; E)
; E) 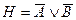 .
.
40. Логическим следствием формул 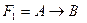 и
и 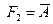 является следующая формула:
является следующая формула:
A) 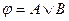 ; B)
; B) 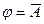 ; C)
; C) 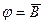 ;
;
D) 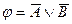 ; E)
; E) 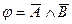 .
.
41. Логическим следствием формул 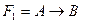 и
и  является следующая формула:
является следующая формула:
A) 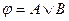 ; B)
; B) 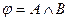 ; C)
; C) 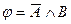 ;
;
D) 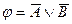 ; E)
; E) 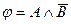 .
.
42. Формула 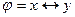 является логическим следствием формулы:
является логическим следствием формулы:
A) 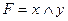 ; B)
; B) 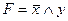 ; C)
; C) 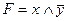 ;
;
D) 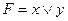 ; E)
; E) 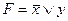 .
.
43. Формула 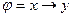 является логическим следствием формулы:
является логическим следствием формулы:
A)  ; B)
; B) 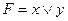 ; C)
; C) 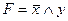 ;
;
D) 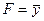 ; E)
; E) 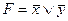 .
.
44. 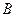 является необходимым, но не достаточным условием для
является необходимым, но не достаточным условием для 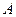 , если истинными являются следующие высказывания:
, если истинными являются следующие высказывания:
A) 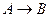 и
и 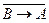 ; B)
; B) 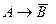 и
и 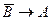 ;
;
C) 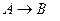 и
и 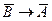 ; D)
; D) 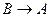 и
и 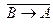 ;
;
E) 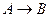 и
и 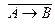 .
.
45. 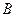 является достаточным, но не необходимым условием для
является достаточным, но не необходимым условием для 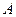 , если истинными являются следующие высказывания…
, если истинными являются следующие высказывания…
46. 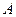 является необходимым, но не достаточным условием для
является необходимым, но не достаточным условием для 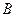 , если следующие высказывания являются истинными…
, если следующие высказывания являются истинными…
47. Следующая равносильность определяет закон Де Моргана:
A) 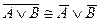 ; B)
; B) 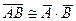 ;
;
C) 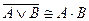 ; D)
; D) 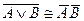 ; E)
; E) 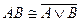 .
.
48. Закон дистрибутивности конъюнкции относительно дизъюнкции имеет вид…
49. Закон дистрибутивности дизъюнкции относительно конъюнкции имеет вид…
50. Следующая формула получена из формулы 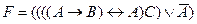 «опусканием» лишних скобок:
«опусканием» лишних скобок:
A) 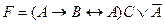 ;
;
B) 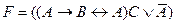 ;
;
C) 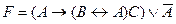 ;
;
D) 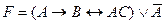 ;
;
E) 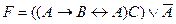 .
.
51. Формула полученная из формулы 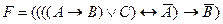 «опусканием» лишних скобок имеет вид…
«опусканием» лишних скобок имеет вид…
52. Формула полученная из формулы 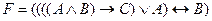 «опусканием» лишних скобок имеет вид…
«опусканием» лишних скобок имеет вид…
53. Правило введения конъюнкции записывается в виде:
A) 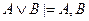 ; B)
; B) 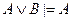 ; C)
; C) 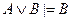 ;
;
D) 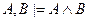 ; E)
; E) 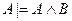 .
.
54. Правило контрапозиции записывается в виде…
55. Правило перестановки посылок записывается в виде…
56. Правило удаления дизъюнкции записывается в виде…
57. Правило силлогизма имеет символическую запись:
A) 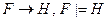 ; B)
; B) 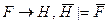 ;
;
C) 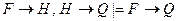 ; D)
; D) 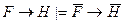 ;
;
E) 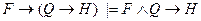 .
.
58. Правило контрапозиции имеет символическую запись…
59. Правило разъединения посылок записывается в виде…
60. Правило соединения посылок записывается в виде…
61. Признак логического следования записывается в виде…
62. Признак равносильности формул 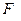 и
и 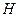 алгебры высказываний записывается в виде…
алгебры высказываний записывается в виде…
63. Формулой равносильной к отрицанию формулы 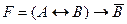 является следующая формула
является следующая формула 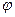 :
:
A) 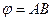 ; B)
; B) 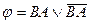 ; C)
; C) 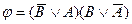 ;
;
D) 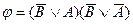 ; E)
; E) 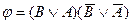 .
.
64. Формулой равносильной к отрицанию формулы 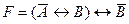 является следующая формула
является следующая формула 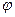 :
:
A) 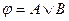 ; B)
; B) 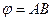 ; C)
; C) 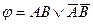 ;
;
D) 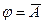 ; E)
; E) 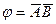 .
.
65. Формулой равносильной к отрицанию формулы 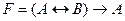 является следующая формула
является следующая формула 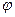 :
:
A) 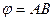 ; B)
; B) 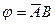 ; C)
; C) 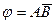 ;
;
D) 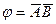 ; E)
; E) 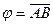 .
.
66. Закон двойственности для формул 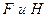 записывается в виде…
записывается в виде…
67. СДНФ для формулы 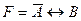 имеет вид:
имеет вид:
A) 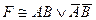 ; B)
; B) 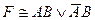 ;
;
C) 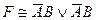 ; D)
; D) 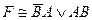 ;
;
E) 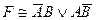 .
.
68. СДНФ для формулы 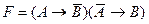 имеет вид…
имеет вид…
69. СКНФ для формулы 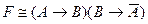 имеет вид…
имеет вид…
70. Формула от трех переменных 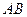 является:
является:
A) СКНФ; B) СДНФ; C) ДНФ; D) КНФ;
E) СДНФ и СКНФ.
71. Формула от трех переменных 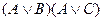 является:
является:
A) СКНФ; B) СДНФ; C) ДНФ; D) КНФ;
E) СДНФ и СКНФ.
72. Формула от трех переменных 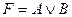 является:
является:
A) СКНФ; B) СДНФ; C) КНФ;
D) СДНФ и СКНФ; E) не является ДНФ.
73. Если СДНФ для формулы 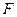 имеет вид
имеет вид 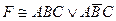 то СКНФ для формулы
то СКНФ для формулы 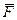 имеет вид:
имеет вид:
A) 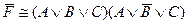 ;
;
B) 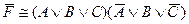 ;
;
C) 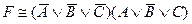 ;
;
D) 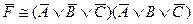 ;
;
E) 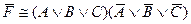 .
.
74. Если СДНФ для формулы 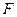 имеет вид
имеет вид 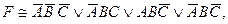 то ее СКНФ имеет вид…
то ее СКНФ имеет вид…
75. Если СКНФ для формулы F, имеет вид 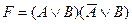 , то ее СДНФ имеет вид…
, то ее СДНФ имеет вид…
76. Релейно – контактная схема, состоящая из двух контактов А,В замкнутая тогда и только тогда, когда замкнут ровно один контакт реализуется с помощью формулы 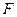 алгебры высказываний:
алгебры высказываний:
A) 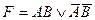 ; B)
; B) 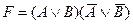 ;
;
C) 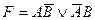 ; D)
; D) 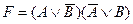 ;
;
E) 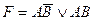 .
.
77. Релейно – контактная схема, состоящая из двух контактов А, В и замкнутая тогда и только тогда, когда замкнуто не более одного контакта реализуется с помощью формулы алгебры высказываний…
78. Релейно – контактная схема, состоящая из трех контактов А, В, С замкнутая тогда и только тогда, когда замкнуто ровно два контакта реализуется с помощью формулы алгебры высказываний…
79. Символическая запись теоремы дедукции (для двух посылок 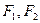 и логического следствия Н) имеет вид:
и логического следствия Н) имеет вид:
A) 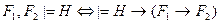 ;
;
B) 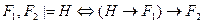 ;
;
C) 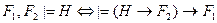 ;
;
D) 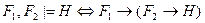 ;
;
E)  .
.
80. Символическая запись теоремы дедукции (для трех посылок 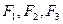 и логического следствия Н) имеет вид…
и логического следствия Н) имеет вид…
81. Символическая запись метода доказательства приведением к абсурду имеет вид:
A) 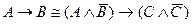 ; B)
; B) 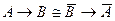 ;
;
C) 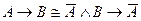 ; D)
; D) 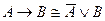 ;
;
E) 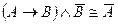 .
.
82. Обоснованием доказательства методом от противного является следующая равносильность…
83. Обоснованием доказательства методом «приведения к абсурду» является следующее логическое следование…
84. Обоснованием доказательства по принципу полной дизъюнкции (для 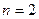 ) является следующее логическое следование…
) является следующее логическое следование…
85. Логическую структуру теоремы: «Если 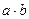 делится на
делится на 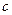 , то из того, что
, то из того, что 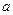 не делится на
не делится на 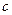 следует, что
следует, что 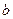 делится на
делится на 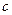 » можно записать в виде…
» можно записать в виде…
86. Логическую структуру теоремы: «Если два угла вписаны в окружность, то из того, что они опираются на одну и ту же дугу следует, что они равны» можно записать в виде…
87. Логическую структуру теоремы: «Если четырех угольник является параллелограммом, то из того, что его диагонали не равны, следует, что он не является прямоугольником» - можно записать в виде…
88. Логическую структуру теоремы противоположной к теореме: Если 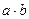 делится на
делится на 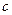 то из того, что
то из того, что 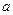 не делится на
не делится на 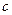 следует, что
следует, что 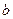 делится на
делится на 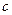 можно записать в виде…
можно записать в виде…
89. Логическую структуру теоремы обратной к теореме: «Если прямая 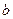 является проекцией прямой
является проекцией прямой 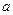 на плоскость
на плоскость 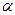 и прямая
и прямая 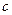 плоскости
плоскости 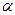 перпендикулярна к
перпендикулярна к 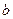 , то и
, то и 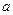 перпендикулярна к
перпендикулярна к 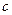 » можно записать в виде…
» можно записать в виде…
90. Логическая структура теоремы противоположной к обратной к теореме выражающей свойство диагоналей ромба имеет вид…
91. Если предложение имеет логическую структуру 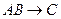 , то предложение противоположное к обратному имеет логическую структуру:
, то предложение противоположное к обратному имеет логическую структуру:
A) 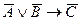 ; B)
; B) 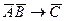 ; C)
; C) 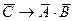 ;
;
D) 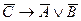 ; E)
; E) 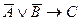 .
.
92. Если предложение имеет логическую структуру 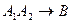 , то ему противоположное имеет логическую структуру…
, то ему противоположное имеет логическую структуру…
93. Если предложение имеет логическую структуру, 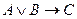 , то противоположное к нему имеет следующую логическую структуру…
, то противоположное к нему имеет следующую логическую структуру…
94. Если предложение имеет логическую структуру 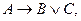 то противоположное к обратному имеет логическую структуру…
то противоположное к обратному имеет логическую структуру…
95. К предложению имеющему логическую структуру 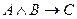 противоположное к обратному имеет логическую структуру…
противоположное к обратному имеет логическую структуру…
96. Равносильным к предложению обратному к теореме имеющей логическую структуру 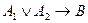 , является предложение имеющее логическую структуру:
, является предложение имеющее логическую структуру:
A) 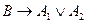 ; B)
; B) 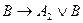 ; C)
; C) 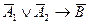 ;
;
D) 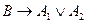 ; E)
; E) 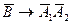 .
.
97. В предложении: «Для того, чтобы произведение двух целых чисел 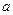 и
и 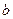 делилось на целое число
делилось на целое число 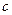 … чтобы оба множителя делились на
… чтобы оба множителя делились на 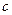 » пропуски заполнены словами:
» пропуски заполнены словами:
A) необходимо и достаточно; B) недостаточно;
C) необходимо, но не достаточно;
D) достаточно, но не необходимо;
E) не необходимо и не достаточно.
98. В предложении «Для того чтобы четырехугольник был прямоугольником …, чтобы его диагонали были равны» пропуски заполнены словами…
99. В предложении: «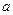 делилось на
делилось на 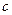 … … для того чтобы
… … для того чтобы 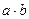 делилось на
делилось на 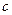 » пропуски заполнены словами…
» пропуски заполнены словами…
100. Заданы три предложения:
а) Если в параллелограмме диагонали взаимно – перпендикулярны, то этот параллелограмм является ромбом.
б) Параллелограмм является ромбом.
в) диагонали параллелограмма взаимно – перпендикулярны.
Тогда верно предложение.
A) Из (а), (б) следует (в); B) Из (а), (в) следует (б);
C) Из (б) следует (в); D) Из (б), (в) следует (а);
E) Из (в) следует (б).
101. Заданы три предложения:
а) если треугольник равнобедренный, то его углы при основании равны и медиана угла при вершине является высотой.
б) углы треугольника попарно не равны.
в) треугольник не равнобедренный или ни одна из его медиан не является и высотой.
Тогда верно предложение:
A) Из (а), (б) следует (в); B) Из (а), (в) следует (б);
C) Из (а) следует (б); D) Из (а) следует (в);
E) Из (б) следует (в).
102. Заданы три предложения:
а) если число делится на5, то оно оканчивается нулем или цифрой 5.
б) данное число делится на 5 и не оканчивается нулем.
в) данное число оканчивается цифрой 5.
Тогда верно предложение.
A) Из (а), (б) следует (в); B) Из (б), (в) следует (а);
C) Из (а), (в) не следует (б); D) Из (а) следует (б);
E) Из (а) следует (в).
103. Если предложение имеет логическую структуру, 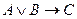 то противоположное к нему имеет следующую логическую структуру
то противоположное к нему имеет следующую логическую структуру
A) 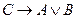 ; B)
; B) 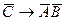 ; C)
; C) 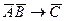 ;
;
D) 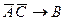 ; E)
; E) 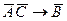 .
.
 2015-01-30
2015-01-30 754
754








