| № варианта | Задание |
| 1. | Дано действительное x. Последовательность a1,a2,… по следующему закону: 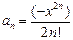 Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. |
| 2. | Вычислить и вывести те члены последовательности, 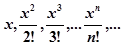 значения которых больше ε = 0.001при x = 0.2. значения которых больше ε = 0.001при x = 0.2. |
| 3. | Вычислитьarctg(x) с точностью ε = 0.0001, воспользовавшись разложением в ряд: 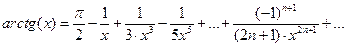 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=1.5. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=1.5. |
| 4. | Вычислитьln(x) с точностью ε = 0.00001, воспользовавшись разложением в ряд: 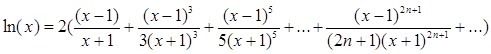 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=0.5. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=0.5. |
| 5. | Вычислить sin 0.5с точностью ε = 0.0001, воспользовавшись разложением в ряд: 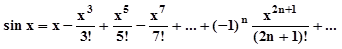 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. |
| 6. | Вычислить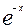 с точностью ε = 0.00001, воспользовавшись разложением в ряд: с точностью ε = 0.00001, воспользовавшись разложением в ряд: 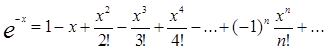 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x =10. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x =10. |
| 7. | Вычислить cos 0.6 с точностью ε = 0.00001, воспользовавшись разложением в ряд: 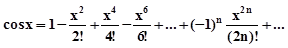 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. |
| 8. | Вычислить и вывести те члены последовательности, 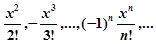 значения которых по модулю больше ε = 0.001 при x = 0.5. значения которых по модулю больше ε = 0.001 при x = 0.5. |
| 9. | Вычислить 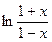 при |x|<1 с точностью до ε = 0.0001, воспользовавшись разложением в ряд: при |x|<1 с точностью до ε = 0.0001, воспользовавшись разложением в ряд: 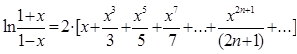 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. |
| 10. | Вычислить и вывести те члены последовательности, 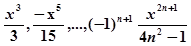 значения которых по модулю больше ε = 0.001 при x = 0.3. значения которых по модулю больше ε = 0.001 при x = 0.3. |
| 11. | Вычислитьln(x) с точностью ε = 0.0001, воспользовавшись разложением в ряд: 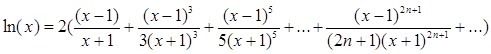 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=1.5. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=1.5. |
| 12. | Вычислить sh 0.3 с точностью до ε= 0.00005, воспользовавшись разложением в ряд: 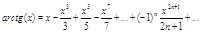 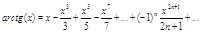 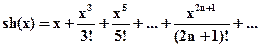 Сравнить результат со значением, полученным с помощью встроенной функции для вычисления ex, используя соотношение: Сравнить результат со значением, полученным с помощью встроенной функции для вычисления ex, используя соотношение: 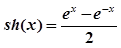 |
| 13. | Дано действительное x. Последовательность a1,a2,… по следующему закону: 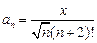 Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. |
| 14. | Вычислить ch 0.7 с точностью до ε = 0.00005, воспользовавшись разложением в ряд: 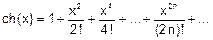 Сравнить результат со значением, полученным с помощью встроенной функции Сравнить результат со значением, полученным с помощью встроенной функции  , используя соотношение: , используя соотношение: 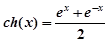 |
| 15. | Вычислить приближенное значение бесконечной суммы с точностью ε=0,0001 (справа от суммы дается выражение для проверки полученного результата): 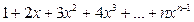 (для |x|<1 сумма равна (для |x|<1 сумма равна 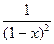 ) ) |
| 16. | Вычислить 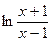 при |x|>1 с точностью до ε = 0.0001, воспользовавшись разложением в ряд: при |x|>1 с точностью до ε = 0.0001, воспользовавшись разложением в ряд: 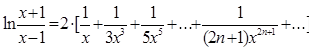 Сравнить результат с табличным значением. Сравнить результат с табличным значением. |
| 17. | Вычислитьln(x+1) с точностью ε = 0.0001, воспользовавшись разложением в ряд: 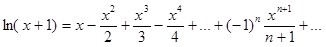 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=0.5. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=0.5. |
| 18. | Вычислить и вывести те члены последовательности, 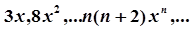 , значения, которых больше ε = 0.01, при x = 0.6. , значения, которых больше ε = 0.01, при x = 0.6. |
| 19. | Вычислить приближенное значение бесконечной суммы с точностью ε=0,0001 (справа от суммы дается ее точное значение, с которым можно сравнить полученный результат): 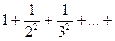 p2/6. p2/6. |
| 20. | Дано действительное x. Последовательность a1,a2,… по следующему закону: 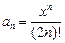 Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. |
| 21. | Вычислить приближенное значение бесконечной суммы с точностью ε=0,0001 (справа от суммы дается ее точное значение, с которым можно сравнить полученный результат): 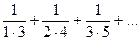 3/4. 3/4. |
| 22. | Вычислить приближенное значение бесконечной суммы с точностью ε=0,0001 (справа от суммы дается ее точное значение, с которым можно сравнить полученный результат):  1/4. 1/4. |
| 23. | Вычислить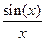 с точностью ε = 0.0001, воспользовавшись разложением в ряд: с точностью ε = 0.0001, воспользовавшись разложением в ряд:  . Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=0.5. . Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=0.5. |
| 24. | Дано действительное x. Последовательность a1,a2,… по следующему закону:  Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. |
| 25. | Дано действительное x. Последовательность a1,a2,… по следующему закону: 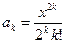 Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. |
| 26. | Вычислить приближенное значение бесконечной суммы с точностью ε=0,0001 (справа от суммы дается ее точное значение, с которым можно сравнить полученный результат): 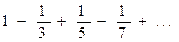 p/4 p/4 |
| 27. | Дано действительное x. Последовательность a1,a2,… по следующему закону:  Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. |
| 28. | Вычислить ln(2) с точностью ε = 0.001, воспользовавшись представлением в виде ряда: 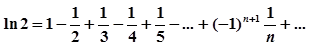 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. |
| 29. | Дано действительное x. Последовательность a1,a2,… по следующему закону: 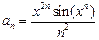 Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. Получить a1+…+ak, где k- наименьшее целое число, удовлетворяющее двум условиям k>10 и |ak+1|<10-5. |
| 30. | Вычислить с точностью ε = 0.00001 константу Эйлера (основание натурального логарифма), воспользовавшись разложением в ряд: 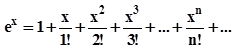 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. |
Задание 5. Составить алгоритм
|
|

Сейчас читают про:
 2015-01-30
2015-01-30 1656
1656







