2015-01-30
1462
Основное свойство данной функции — постоянная эластичность замещения. А именно, можно показать, что эластичность замещения для данной функции равна
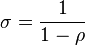
Если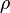 
стремится к нулю, то данная функция стремится к производственной функции Кобба-Дугласа, эластичность замещения которой как раз равна 1. Если 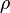стремится к бесконечности, то имеем функцию с нулевой эластичностью замещения — производственную функцию Леонтьева.
Таблица 29.2. Производственные функции с постоянной эластичностью замещения факторов (CES)
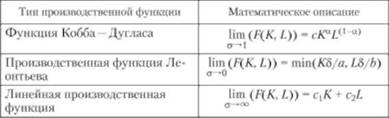
1. Производственная функция Кобба-Дугласа. Первый успешный опыт построения производственной функции, как уравнения регрессии на базе статистических данных, был получен американскими учеными - математиком Д. Коббом и экономистом П. Дугласом в 1928 году. Предложенная ими функция изначально имела вид:
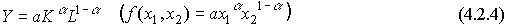
где Y - объем выпуска, K - величина производственных фондов (капитал), L - затраты труда,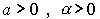 
- числовые параметры (масштабное число и показатель эластичности). Благодаря своей простоте и рациональности, эта функция широко применяется до сих пор и получила дальнейшие обобщения в различных направлениях. Функцию Кобба-Дугласа иногда мы будем записывать в виде
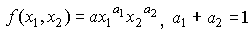
Легко проверить, что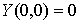 
и
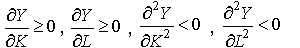
Кроме того, функция (4.2.4) линейно-однородна:
.
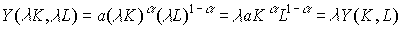Таким образом, функция Кобба-Дугласа (4.2.4) обладает всеми вышеуказанными свойствами.
Для многофакторного производства функция Кобба-Дугласа имеет вид:
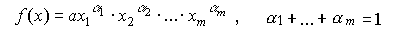
Для учета технического прогресса в функцию Кобба-Дугласа вводят специальный множитель (технического прогресса)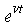 
, где t - параметр времени, 
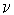- постоянное число, характеризующее темп развития. В результате функция принимает "динамический" вид:
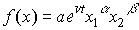
где не обязательно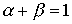 
. Как будет показано в следующем параграфе, показатели степени в функции (4.2.4) имеют смысл эластичности выпуска по капиталу и труду.
2. Производственная функция затрат-выпуска (функция Леонтьева) получается из (4.2.6) при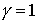 
:
Содержательно эта функция задает пропорцию, с помощью которой определяется количество затрат каждого вида, необходимое для производства одной единицы выпускаемой продукции. Поэтому в литературе часто встречаются другие формы записи:
или
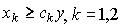
Здесь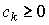 
- количество затрат вида k, необходимое для производства одной единицы продукции, а y - выпуск.
3. Линейная производственная функция (функция с взаимозамещением ресурсов) применяется при наличии линейной зависимости выпуска от затрат:
где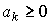 
- норма затрат k -го вида для производства единицы продукции (предельный физический продукт затрат).
