И.М. Тришин
Теория вероятностей
Тема 1. Основные понятия и теоремы теории
Вероятностей
Понятие случайного события
Испытанием мы будем называть тип опыта (эксперимента).
Например, извлечение наудачу карты из колоды – испытание.
Бросание наудачу игральной кости (монеты) – испытание.
Существенно, что испытания в приведенных примерах (как и все испытания в данном курсе) выполняются наудачу, т.е. субъективный фактор здесь предполагается исключенным.
Определение. Случайным событием называется выделенный исход некоторого испытания.
Очевидно, что в конкретном испытании рассматриваемое случайное событие может наступить, а может и не наступить. (Отметим также, что сам эпитет “случайное”  перед термином “событие“ в дальнейшем для краткости мы обычно будем опускать.)
перед термином “событие“ в дальнейшем для краткости мы обычно будем опускать.)
Всюду ниже для обозначения событий мы будем использовать заглавные буквы 
 латинского алфавита (возможно, с индексами). Например,
латинского алфавита (возможно, с индексами). Например, 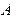 , B,C,¼
, B,C,¼  или
или 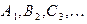 .
.
Пример. Пусть испытание – извлечение карты из колоды. Тогда событиями являются: A – извлечена карты красной масти, B – извлечена “ картинка“, C – извлечен туз и т.п. Если в результате конкретного испытания из колоды достали, например, семерку бубен, то событие A наступило, события B и C – нет.
Пример. Пусть испытание – бросание игральной кости. Тогда событиями являются, например, A –  число выпавших очков – четно, B – число выпавших очков – больше 4, C– на верхней грани игральной кости выпала “5”.
число выпавших очков – четно, B – число выпавших очков – больше 4, C– на верхней грани игральной кости выпала “5”.
Удобным обозначением для событий, относящихся к рассматриваемому испытанию (бросание игральной кости), служит перечисление всех исходов благоприятствующих наступлению события. Например, здесь 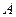 ={2,4,6},
={2,4,6}, 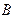 ={5,6},
={5,6}, 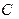 ={5}.
={5}.
1.2. Статистическое определение вероятности 

Пусть проведено N испытаний, в которых некоторое событие A наступает 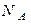 раз. Тогда отношение
раз. Тогда отношение 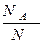 называется частостью (долей) наступления события A в N испытаниях.
называется частостью (долей) наступления события A в N испытаниях.
Определение. Пусть условия проведения некоторого испытания можно в точности воспроизвести неограниченное число раз. Тогда вероятностью 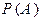 наступления события A (в одном испытании) называется такое число, около которого группируются значения частости
наступления события A (в одном испытании) называется такое число, около которого группируются значения частости 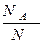 при неограниченном увеличении числа
при неограниченном увеличении числа  испытаний N.
испытаний N.
Символически это определение можно записать в виде
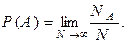
Отметим практическое следствие данного определения: если нас интересует значение вероятности наступления некоторого события 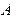 , то производят достаточно большое число испытаний N, по их результатам определяют значение частости
, то производят достаточно большое число испытаний N, по их результатам определяют значение частости 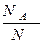 и затем полагают
и затем полагают

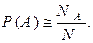
(Более подробно обоснование такого подхода будет рассмотрено ниже: см. Закон больших чисел, теорему Бернулли.)
Также статистическое определение вероятности имеет следующее важное
Следствие (область возможных значений вероятности события). Значение вероятности произвольного события 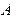 заключено в границах от 0 до 1, т.е.
заключено в границах от 0 до 1, т.е.
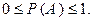
Доказательство. Очевидно, что
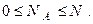
Выполняя почленное деление последнего неравенства на 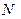 , получаем
, получаем
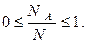
Переходя теперь к пределу при 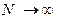 , имеем
, имеем
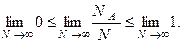
 2015-01-30
2015-01-30 990
990







