Плотность распределения непрерывной случайной величины

Неформально говоря, случайная величина непрерывна, если ее значения полностью заполняют некоторый интервал. Более точно, справедливо

Определение. Случайная величина называется непрерывной,если ее функция распределения непрерывна на всей числовой прямой и дифференцируема при всех х за исключением, быть может, отдельных значений.

Определение. Плотностью распределения непрерывной случайной величины Х называется такая функция 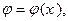что вероятность того, что в произвольном испытании значение случайной величины Х окажется принадлежащим некоторому отрезку 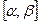, вычисляется по формуле

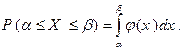
Принимая во внимание геометрический смысл определенного интеграла, получаем

Геометрический смысл плотности распределения. Вероятность того, что в произвольном испытании значение случайной величины Х окажется принадлежащим некоторому отрезку 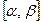, численно равна площади 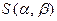под кривой плотности распределения на данном отрезке (см. рис. 4).

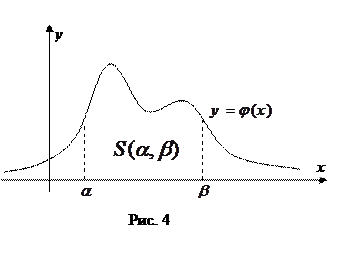
Пример. Пусть плотность распределения случайной величины Х имеет вид:

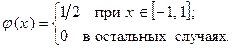
Найти вероятности:

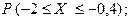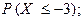а) б) в)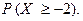

Решение. а)По определению плотности распределения,

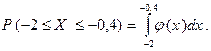
Вместе с тем, данная плотность распределения задана аналитически по-разному на промежутках 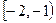и 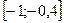отрезка интегрирования. Соответственно, используя свойства определенного интеграла, получаем

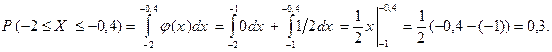
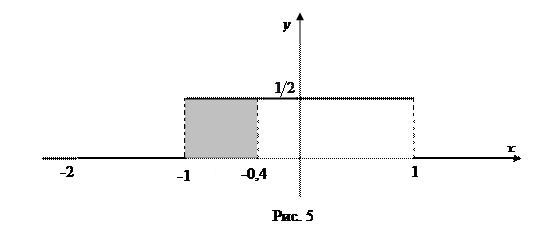
По геометрическому смыслу плотности распределения, полученная вероятность численно равна площади под кривой плотности распределения (см. рис. 5) на отрезке 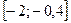, т.е. равна площади фигуры, составленной из отрезка длины 1 и прямоугольника со сторонами 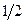и 0,6.

б) Неравенство 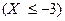равносильно тому, что 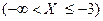. Учитывая, что на промежутке 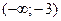данная плотность распределения равна 0, получаем

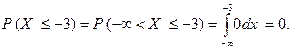
в) Аналогично предыдущим пунктам задачи, имеем

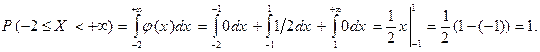
Рассмотрение геометрического смысла результатов последних двух пунктов данного примера мы оставляем читателю в качестве упражнения. ▶