Определение 1. Законом распределения вероятностей дискретной двумерной случайной величины называют перечень возможных значений этой величины (т.е. пар чисел 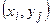 (
(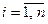 ,
,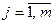 ) и их вероятностей
) и их вероятностей  ).
).
Замечание 1. Обычно закон распределения дискретной двумерной случайной величины задают в виде таблицы. Первая строка таблицы содержит все возможные значения составляющей У, а первый столбец – все возможные значения составляющей Х. В клетке, стоящей на пересечении 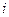 -го столбца и
-го столбца и  -ой строки указана вероятность
-ой строки указана вероятность  того, что двумерная случайная величина
того, что двумерная случайная величина 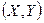 примет значение
примет значение 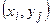 .
.
| У Х | 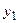 |  | … | 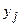 | … |  |
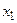 |  |  | … | 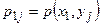 | … |  |
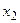 |  |  | … |  | … |  |
| … | … | … | … | … | … | … |
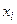 | 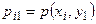 | 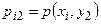 | … |  | … | 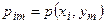 |
| … | … | … | … | … | … | … |
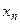 |  | 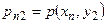 | … |  | … |  |
Возможно также задание закона распределения двумерной случайной величины, когда первая строка таблицы содержит все возможные значения составляющей Х, а первый столбец – все возможные значения составляющей У. Соответствующие значения вероятностей «транспонируются» относительно приведённой таблицы.
Замечание 2. Так как события  (
(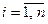 ,
,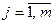 ) образуют полную группу попарно несовместных событий, то сема вероятностей, помещённых во всех клетках таблицы, равна единице:
) образуют полную группу попарно несовместных событий, то сема вероятностей, помещённых во всех клетках таблицы, равна единице:  .
.
|
|
|
Замечание 3. Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих. Действительно, распределение одномерной случайной величины Х можно получить, вычислив вероятность события  (
(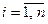 ) как сумму вероятностей несовместных событий:
) как сумму вероятностей несовместных событий:  (т.е. нужно просуммировать вероятности в каждой строке
(т.е. нужно просуммировать вероятности в каждой строке 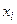 (
(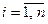 )).
)).
Аналогично определяется распределение одномерной случайной величины У: 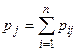 (т.е. нужно просуммировать вероятности в каждом столбце
(т.е. нужно просуммировать вероятности в каждом столбце 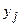 (
(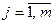 )).
)).
Если зафиксировать значение аргумента У ( ), то при этом случайная величина Х может принять одно из своих возможных значений
), то при этом случайная величина Х может принять одно из своих возможных значений 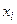 (
(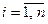 ). Вероятности этих значений при
). Вероятности этих значений при  , вообще говоря, не будут равны вероятностям
, вообще говоря, не будут равны вероятностям  .
.
Определение 2. Условным распределением составляющей Х при условии  называется совокупность условных вероятностей
называется совокупность условных вероятностей  (
(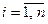 ), вычисленных в предположении, что событие
), вычисленных в предположении, что событие  уже наступило (
уже наступило ( фиксировано при любых значениях Х).
фиксировано при любых значениях Х).
Вероятности 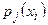 этого распределения являются условными вероятностями события
этого распределения являются условными вероятностями события  , найденными в предположении, что событие
, найденными в предположении, что событие  произошло. Из определения условной вероятности
произошло. Из определения условной вероятности 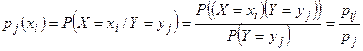 .
.
Аналогично условное распределение случайной величины У при условии  задаётся с помощью условных вероятностей:
задаётся с помощью условных вероятностей:
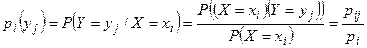 .
.
Замечание 4. Иногда для условных распределений используются обозначения 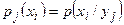 и
и  .
.
Замечание 5. Сумма вероятностей условного распределения равна 1.
Доказательство. Так как при фиксированном 
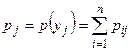 , то
, то 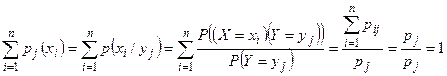 . Аналогично доказывается, что при фиксированном
. Аналогично доказывается, что при фиксированном 
 .
.
Пример. Закон распределения дискретной двумерной случайной величины задан таблицей:
|
|
|
| У Х | 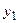 =1 =1 |  =2 =2 |
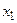 =-1 =-1 | 0,10 | 0,06 |
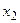 =0 =0 | 0,30 | 0,18 |
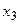 =1 =1 | 0,20 | 0,16 |
Найти: 1) законы распределения составляющих двумерной случайной величины, 2) условные законы распределения случайной величины Х при условии  и случайной величины У при условии
и случайной величины У при условии 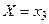 ; 3) вероятность
; 3) вероятность  .
.
Решение. 1) Закон распределения Х: просуммировать элементы в строках, составить таблицу. Закон распределения У: просуммировать элементы в столбцах, составить таблицу.
2) Закон распределения Х при условии  : вероятности, стоящие во 2-м столбце разделить на их сумму. Составить таблицу. Закон распределения У при условии
: вероятности, стоящие во 2-м столбце разделить на их сумму. Составить таблицу. Закон распределения У при условии 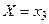 : вероятности, стоящие в 3-ей строке, разделить на их сумму. Составить таблицу.
: вероятности, стоящие в 3-ей строке, разделить на их сумму. Составить таблицу.
3) Для нахождения вероятности  складываем вероятности тех пар
складываем вероятности тех пар 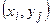 , для которых
, для которых 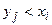 .
.
 2014-02-02
2014-02-02 4310
4310
