Проверить гипотезу о наличии гомоскедастичности, устранить ее и построить уравнений линейной регрессии.
| x | y | x | y | x | y | x | y | x | y |
| 75,5 | 80,5 | 85,5 | |||||||
| 75,5 | 88,5 | 93,5 | 105,5 | ||||||
| 77,5 | 84,5 | 97,5 | |||||||
| 78,5 | 110,5 | ||||||||
| 85,5 | 102,5 | ||||||||
| 86,5 | 118,5 |
Уравнение регрессии имеет вид 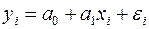 . Мы видим, что с ростом x разброс значений y увеличивается. Например, при
. Мы видим, что с ростом x разброс значений y увеличивается. Например, при 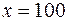 размах вариации переменной y равен
размах вариации переменной y равен 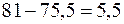 , а при
, а при 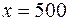 размах вариации переменной y равен
размах вариации переменной y равен 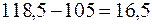 . Поэтому можно ожидать наличие гетероскедастичности.
. Поэтому можно ожидать наличие гетероскедастичности.
Проверим с помощью теста Голдфелда-Квандта гипотезу о наличии гетероскедастичности. Возьмем 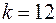 . Доверительная вероятность
. Доверительная вероятность 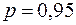 , тогда
, тогда 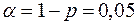 , с помощью функции FРАСПОБР(0,05;10;10) находится граничная точка
, с помощью функции FРАСПОБР(0,05;10;10) находится граничная точка 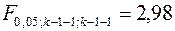 . m ¾ это количество факторов модели, в нашем случае m = 1.
. m ¾ это количество факторов модели, в нашем случае m = 1.
Теперь воспользуемся Пакетом анализа и заполним таблицу:
| x | y | 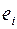
| 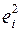
| x | y | 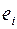
| 
|
| 75,5 | ¾1,15 | 1,32 | ¾7,03 | 49,35 | |||
| 75,5 | ¾1,15 | 1,32 | 93,5 | ¾6,53 | 42,58 | ||
| 77,5 | 0,85 | 0,72 | 97,5 | ¾2,53 | 6,38 | ||
| 78,5 | 1,85 | 3,42 | ¾1,03 | 1,05 | |||
| 3,35 | 11,22 | 102,5 | 2,47 | 6,13 | |||
| 4,35 | 18,92 | 4,97 | 24,75 | ||||
| 80,5 | ¾3,94 | 15,54 | ¾5,82 | 33,83 | |||
| ¾2,94 | 5,96 | 105,5 | ¾2,32 | 5,37 | |||
| 84,5 | 0,06 | ¾0,82 | 0,67 | ||||
| 0,56 | 0,31 | 110,5 | 2,68 | 7,2 | |||
| 85,5 | 1,06 | 1,12 | 7,18 | 51,6 | |||
| 86,5 | 2,06 | 4,24 | 118,5 | 10,68 | 114,13 | ||
| Сумма | 64,11 | Сумма | 343,03 | ||||
| 85,5 | ¾6,73 | 45,34 | |||||
| 88,5 | ¾3,73 | 13,94 | |||||
| ¾2,23 | 4,99 | ||||||
| ¾1,23 | 1,52 | ||||||
| 2,77 | 7,65 | ||||||
| 3,77 | 14,19 |
Столбец 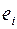 ¾ это столбец Остатки из блока Вывод остатка.
¾ это столбец Остатки из блока Вывод остатка.
Суммы квадратов отклонений соответственно равны: 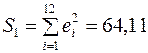 ,
, 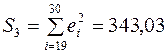 . Значения из середины таблицы при
. Значения из середины таблицы при 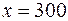 в вычислении сумм не используются.
в вычислении сумм не используются.
Статистика определяется формулой 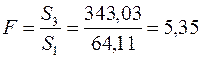 . Так как 5,35 > 2,98, то на уровне значимости 5% принимается гипотеза о наличии гетероскедастичности.
. Так как 5,35 > 2,98, то на уровне значимости 5% принимается гипотеза о наличии гетероскедастичности.
Устраним гетероскедастичность. Предположим, что неизвестные дисперсии отклонений 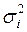 неизвестны и пропорциональны
неизвестны и пропорциональны 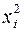 .
.
Уравнений линейной регрессии имеет вид 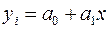 . Разделим обе части этого уравнения на
. Разделим обе части этого уравнения на 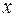 . Тогда получаем
. Тогда получаем 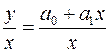 , откуда
, откуда 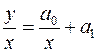 . Обозначим
. Обозначим 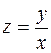 ,
, 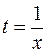 . Получаем уравнение
. Получаем уравнение 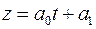 . Заполним таблицу:
. Заполним таблицу:
| x | y | 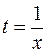
| 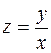
| x | y | 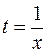
| 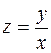
|
| 75,5 | 0,01 | 0,76 | 0,0025 | 0,23 | |||
| 75,5 | 0,01 | 0,76 | 93,5 | 0,0025 | 0,23 | ||
| 77,5 | 0,01 | 0,78 | 97,5 | 0,0025 | 0,24 | ||
| 78,5 | 0,01 | 0,79 | 0,0025 | 0,25 | |||
| 0,01 | 0,8 | 102,5 | 0,0025 | 0,26 | |||
| 0,01 | 0,81 | 0,0025 | 0,26 | ||||
| 80,5 | 0,005 | 0,4 | 0,002 | 0,2 | |||
| 0,005 | 0,41 | 105,5 | 0,002 | 0,21 | |||
| 84,5 | 0,005 | 0,42 | 0,002 | 0,21 | |||
| 0,005 | 0,43 | 110,5 | 0,002 | 0,22 | |||
| 85,5 | 0,005 | 0,43 | 0,002 | 0,23 | |||
| 86,5 | 0,005 | 0,43 | 118,5 | 0,002 | 0,24 | ||
| 85,5 | 0,003 | 0,29 | |||||
| 88,5 | 0,003 | 0,3 | |||||
| 0,003 | 0,3 | ||||||
| 0,003 | 0,3 | ||||||
| 0,003 | 0,32 | ||||||
| 0,003 | 0,32 |
По данным столбцов 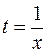 и
и 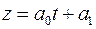 с помощью пакета анализа находим коэффициенты
с помощью пакета анализа находим коэффициенты 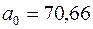 и
и 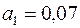 . Тогда уравнение регрессии имеет вид
. Тогда уравнение регрессии имеет вид 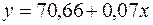 .
.
 2015-01-30
2015-01-30 372
372








