Пример 10

Проверить гипотезу об отсутствии гетероскедастичности с помощью тестов ранговой корреляции Спирмена и теста Голдфелда-Квандта. Доверительная вероятность 95%.

Решение.

Проверим гипотезу с помощью теста Спирмена.

С помощью пакета Анализ данных определяем коэффициенты уравнения линейной регрессии и величины остатков. Получаем уравнение регрессии 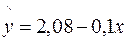. Заполняем таблицу:

x	y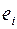
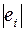
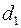
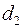
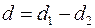
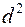
	1,9	0,013
	1,7	¾0,09	0,09
	1,8	0,11	0,12
	1,6	0,003	0,03			¾3
	1,4	¾0,1	0,06
	1,5	0,097	0,097
	1,3	¾0,007	0,007			¾5
	1,2	¾0,01	0,01			¾5
	1,1	¾0,013	0,013			¾4

Второй столбец 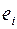¾ это столбец Остатки из блока Вывод остатка. Столбцы 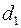и 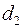содержат порядковые номера элементов столбцов x и 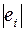, ранжированных по убыванию. Для вычисления значени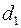й и 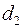можно воспользоваться функцией РАНГ(число;ссылка;0).

Далее вычисляем .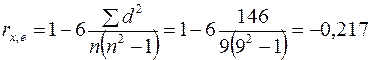

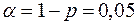. С помощью функции СТЬЮДРАСПОБР(a; n ¾2) находим граничную точку 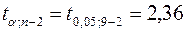. Статистику определяем по формуле 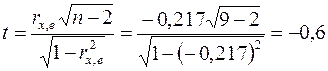. Так как 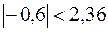, то на уровне значимости 5% принимается гипотеза об отсутствии гетероскедастичности.

Теперь проверим гипотезу с помощью теста Голдфелда-Квандта.

Наша выборка уже упорядочена по величине x. Разделим ее на три группы при k = 3. Вычисляем суммы квадратов отклонений значений из первой и третьей группы.

Первая группа:

x	y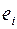
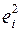
	1,9
	1,7	¾0,09	0,0081
	1,8	0,11	0,012
			0,0202

Третья группа:

x	y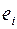
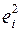
	1,3	¾0,007	0,00005
	1,2	¾0,01	0,0001
	1,1	¾0,013	0,00017
			0,00032

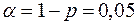, с помощью функции FРАСПОБР(0,05;1;1) находится граничная точка 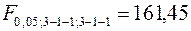. m ¾ это количество факторов модели, в нашем случае m = 1. Статистика определяется формулой 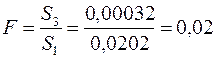. Так как 0,02 < 161,45, то на уровне значимости 5% принимается гипотеза об отсутствии гетероскедастичности.