2015-01-30
430
Рассмотрим линейную регрессию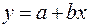 
. Предположим, что стандартное отклонение 
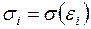пропорционально значению переменной x в этом наблюдении: 
, 
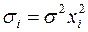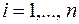. Еще предполагаем, что 
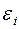имеет нормальное распределение и отсутствует автокорреляция (проблема автокорреляции будет рассмотрена далее). Считаем, что все n наблюдений упорядочиваются по величине x. Эта упорядоченная выборка делится на три примерно равные части объемов k, n ¾ 2k и k соответственно.
Для каждой из выборок объема k оценивается свое уравнение регрессии и находятся суммы квадратов отклонени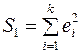й 
и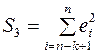 
соответственно.
Доверительная вероятность p,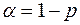 
. С помощью функции FРАСПОБР(
; 
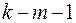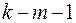; ) находится граничная точка 
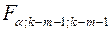, где m ¾ количество факторов модели. Статистика определяется формулой 
.
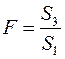Если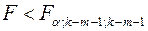 
, то на уровне значимости a принимается гипотеза об отсутствии гетероскедастичности. Иначе гипотеза об отсутствии гетероскедастичности отклоняется. Для множественной регрессии тест обычно проводится для того фактора, который в максимальной степени связан с 
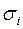. При этом выбирают 
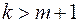. Если нет уверенности относительно выбора фактора 
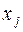, то данный тест можно осуществить для каждого фактора.
