Критерий Дарбина-Уотсона

Это наиболее известный способ обнаружения автокорреляции первого порядка. Пусть n ¾ число наблюдений, m ¾ число факторов модели, a = 0,05 ¾ уровень значимости. По таблицам распределения Дарбина-Уотсона определяются числа 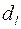и .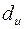

Статистика Дарбина-Уотсона определяется формулой .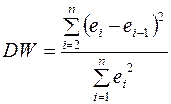

Если 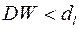, то это свидетельствует о положительной автокорреляции остатков.

Если 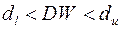, то гипотеза об отсутствии автокорреляции остатков не может быть ни принята, ни отвергнута.

Если 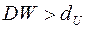, то автокорреляции нет.

Если 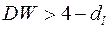, то это свидетельствует об отрицательной автокорреляции остатков.

Если 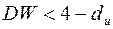, то автокорреляции нет.

Если 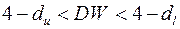, то гипотеза об отсутствии автокорреляции остатков не может быть ни принята, ни отвергнута.

Ограничения при использовании критерия Дарбина-Уотсона:

1) ;

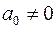2) случайные отклонения определяются формулой 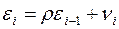, где 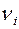¾ случайный коэффициент;

3) статистические данные должны иметь одинаковую периодичность (не должно быть пропусков в наблюдениях);

4) среди факторов не должно быть лаговых переменных, то есть переменных, влияние которых характеризуется определенным запаздыванием.