№ 1. Первый индивид произвел 200 ед. блага А, а второй – 24 0 ед. блага В. Предпочтения индивидов относительно данных благ отображаются функциями полезности: 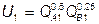 ,
, 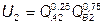 . Индивиды договорились о распределении блага А: QA 1 = 120; QА 2 = 80.
. Индивиды договорились о распределении блага А: QA 1 = 120; QА 2 = 80.
1. Сколько блага В должен получить 1-й индивид для достижения оптимального по Парето распределения благ?
2. При какой цене блага А рынок обеспечивает оптимальное по Парето распределение, если РВ = 1?
Решение
1. Условие оптимального по Парето распределения 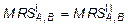 :
:
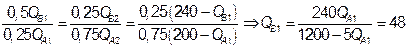 .
.
2. Условие равновесия потребителя:
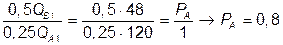 .
.
Бюджет 1-го индивида 0,8×120 + 48 = 144; бюджет 2-го 0,8×80 + 192 = 256.
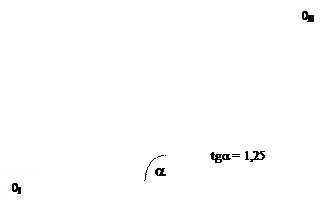
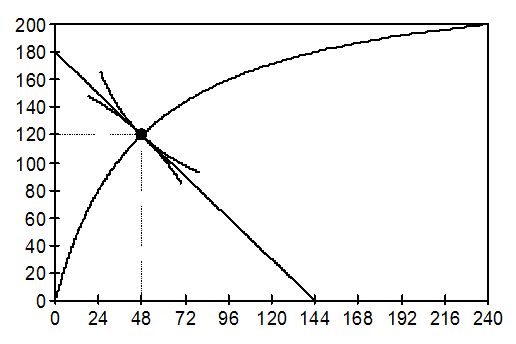
Рис. 6.1. Парето-оптимальность в обмене
№ 2. Кривая производственных возможностей описывается уравнением 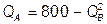 , а функция общественной полезности:
, а функция общественной полезности: 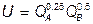 . Определите оптимальные объемы производства каждого блага.
. Определите оптимальные объемы производства каждого блага.
Рассмотрим два способа решения.
Первый способ:
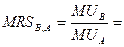
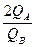
MRTP=(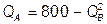 )′= [ - 2
)′= [ - 2 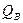 ]=2
]=2 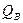
MRS=MRTP
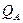 = 400
= 400
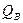 = 20
= 20
Второй способ:
Решение
Производственные возможности выступают в роли бюджетного ограничения при максимизации функции полезности:
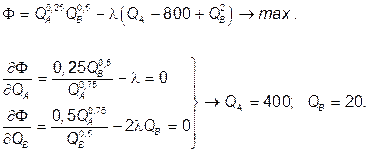

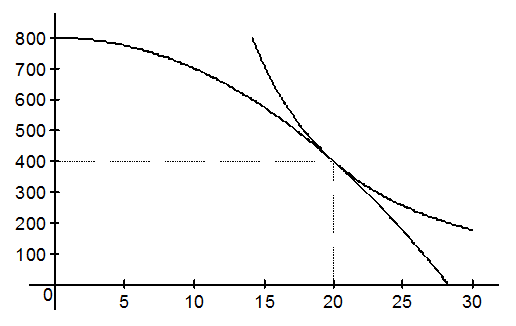
Рис. 6.2. Оптимум в производстве и обмене
№ 3. Опрос показал, что готовность жильцов трех домов платить за озеленение их двора выражается следующими функциями: P 1 = 80 – Q; P 2 = 60 – Q; P3 = 40 – Q, где Pi – максимальная сумма денег, которую согласны заплатить жильцы i -го дома за очередное дерево. Общие затраты на озеленение определяются по формуле TC = 10 + 2 Q + 0,5 Q 2. Определите Парето-оптимальное число деревьев во дворе дома.
Решение
Оптимальное количество деревьев определяется точкой пересечения линий предельных затрат MC = 2 + Q и предельной общественной полезности. Последняя образуется в результате вертикального сложения графиков цены спроса жителей трех домов:
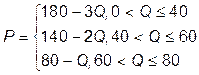
Координаты точки пересечения определяются из равенства: 2 + Q = 140 – 2 Q Þ Q =46. Приравнивание к другим участкам кривой общественной полезности дает решение, не совпадающее с соответствующими интервалами выпуска: 2 + Q = 180 – 3 Q Þ Q = 44,5; 2 + Q = 80 – Q Þ Q = 39.

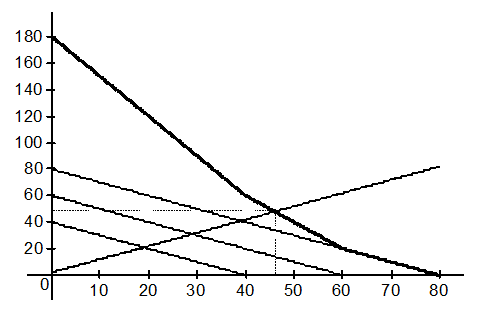
Рис. 6.3. Оптимальный объем выпуска общественного блага
№ 4. Готовность платить за обучение в вузе описывается функцией P = 60 – 0,4N, где P – размер оплаты (млн ден. ед.), а N – число готовых платить (млн чел.). Предельная внешняя выгода от образования, выраженная в деньгах, имеет вид: MU = 80 – 0,4N. Общие затраты образовательного учреждения по подготовке специалистов: TC = 20N + N2.
а) Определить величину внешнего эффекта.
б) Рассчитать число студентов, соответствующее максимуму полезности молодежи и максимуму общественной полезности.
в) Рассчитать величину платы за обучение и дотации, соответствующие максимальной общественной полезности от обучения в вузе.
Решение
а) величина внешнего эффекта (80 – 0,4 N)-(60 – 0,4 N) = 20.
б) из равенства Р = МС число студентов будет
60 – 0,4 N = 20 + 2 N → N = 16.
из равенства MU = МС следует, что
80 – 0,4 N = 20 + 2 N → N = 25.
в) (60 – 0,4*25) = 50.
(20 + 2*25) = 70.
Следовательно, величина дотации будет 20 ден. ед.
№ 5. Спрос на напитки в жестяных банках отображается функцией QD = 200 – 2 P. Общие затраты фирмы на выпуск напитков соответствуют функции TCn = 2 Q + 0,25 Q 2, а зависимость затрат на уборку городского мусора от количества купленных напитков выражается функцией TCu = 0,2 Q 2. Насколько выпуск напитков превышает общественный оптимум, когда расходы на уборку мусора финансирует муниципалитет?
Решение

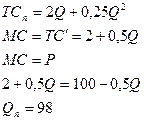
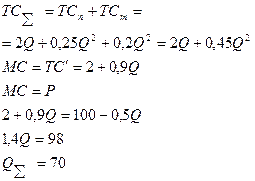
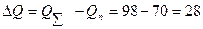
№ 6. На двух взаимосвязанных рынках спрос и предложение отображаются следующими функциями:
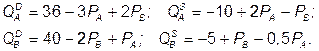
При каких ценах на обоих рынках одновременно устанавливается равновесие?
Решение
Уравнение линии цен частичного равновесия на рынке блага А
36-3 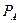 +2
+2 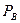 = -10+2
= -10+2 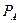 -
- 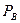
Уравнение линии цен частичного равновесия на рынке блага В
40 - 2 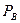 +
+ 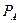 = -5+
= -5+ 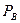 - 0,5
- 0,5 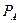
Общее равновесие достигается при:
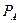 =26
=26
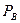 =28
=28
№ 7. При существовании двух изолированных рынков спрос на них отображался соответственно:
QD A= 100 – 4РA; QS A= -20 + 2РA
QD B= 80 - 3РB; QS B= -10 + 3РB
Когда оба товара стали продаваться в одном и том же месте, то функции спроса и предложения приобрели следующий вид:
QD A= 100 - 4РA + 3РB; QS A= -20 + 2РA - РB
QD B= 80 - 3РB + 2РA; QS B= -10 + 3РB - 2РA
Определить:
а) На сколько единиц изменился объем продаж товара А?
б) Как изменились цены товаров?
Решение
а) 100-4 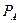 = - 20+2
= - 20+2 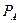
80-3 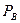 = - 10+3
= - 10+3 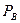
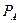 = 20
= 20 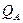 = 20
= 20
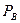 = 15
= 15 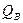 = 35
= 35
80-3 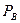 +2
+2 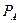 = - 10+3
= - 10+3 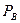 -2
-2 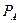
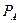 =54
=54
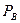 =51
=51
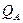 =37
=37
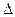
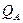 =17
=17
б) 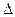
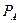 =34
=34
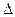
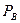 =36
=36
Задачи
№ 1. Предположим, что экономика включает только два предприятия. Одно из них производит товар X, другое – товар Y. На рисунке изображена диаграмма Эджуорта для двух предприятий в пространстве ресурсов «а» и «b».
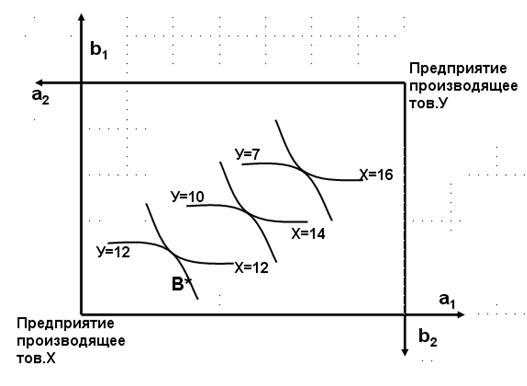
а) Предположим, что распределение ресурсов между предприятиями характеризуется точкой B.
Какое из необходимых условий Парето-оптимального состояния при этом нарушается?
б) Нарисуйте три точки границы производственных возможностей.
№ 2. На рисунке изображена граница возможных благосостояний для двух индивидуумов.
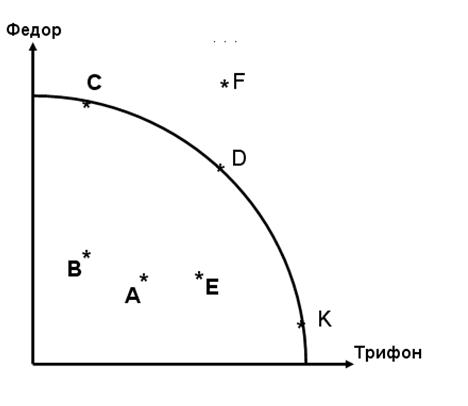
а) Укажите точки, которые являются Парето-оптимальными.
б) Укажите точки, которые являются Парето-предпочтительными по отношению к точке A.
в) Укажите точки, которые являются Парето-предпочтительными по отношению к точке B.
№ 3. Предположим, два потребителя живут в одном городе. Один из продуктов они покупают по одинаковым ценам, а другой – по разным. К нарушению какого из необходимых условий Парето-оптимальности это может привести?
№ 4. Для двух потребителей товары X и Y служат совершенными заменителями в пропорции 1:1. Общее количество товара X – 10 ед., товара Y – 20 ед. Первоначальное распределение товаров таково, что первому потребителю принадлежат 8 ед. товара X и 3 ед. товара Y.
Является ли это распределение Парето - оптимальным?
№ 5. Предположим, два предприятия расположены в одном городе. Один из ресурсов они приобретают по одинаковым ценам, а другой – по разным. К нарушению какого из необходимых условий Парето-оптимальности это может привести?
№ 6. В хозяйстве, располагающем 24 единицами производственного фактора F продукция Q1 производится по технологии Q1 = 4 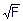 , а продукция Q2 – по технологии Q2 = 2F + 3. Вывести уравнение кривой производственных возможностей.
, а продукция Q2 – по технологии Q2 = 2F + 3. Вывести уравнение кривой производственных возможностей.
№ 7. Производство товаров A и B описывается производственной функцией: QА = 2KL, QВ = 0,5KL. Общий объем используемого труда – 100 ед., капитала – 60 ед.
Построить кривую производственных возможностей.
№ 8. Первый индивид произвел 120 ед. блага А, а второй – 200 ед. блага В. Предпочтения индивидов относительно данных благ отображаются функциями полезности: 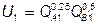 ,
, 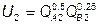 . Индивиды договорились о распределении блага А поровну.
. Индивиды договорились о распределении блага А поровну.
1. Сколько блага В должен получить 1-й индивид для достижения оптимального по Парето распределения благ?
2. При какой цене блага А рынок обеспечивает оптимальное по Парето распределение, если РВ = 1?
№ 9. Предпочтения двух потребителей относительно благ А и В представлены функциями полезности: 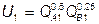 ,
, 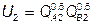 . Первый потребитель имеет 30 ед. блага А, а второй – 120 ед. блага B. Первый потребитель хочет получить от второго 30 ед. блага B в обмен на определенное количество блага А при РВ = 3. Какую максимальную цену онможет установить на благо А?
. Первый потребитель имеет 30 ед. блага А, а второй – 120 ед. блага B. Первый потребитель хочет получить от второго 30 ед. блага B в обмен на определенное количество блага А при РВ = 3. Какую максимальную цену онможет установить на благо А?
№ 10. Предпочтения двух потребителей относительно благ А и В представлены функциями полезности: 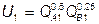 ,
, 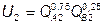 . Первый потребитель имеет 150 ед. блага А, а второй – 120 ед. блага B. Первый потребитель хочет получить от второго 60 ед. блага B в обмен на определенное количество блага А при РВ = 2. Определите бюджет (ценность имеющихся благ) 1-го потребителя после обмена.
. Первый потребитель имеет 150 ед. блага А, а второй – 120 ед. блага B. Первый потребитель хочет получить от второго 60 ед. блага B в обмен на определенное количество блага А при РВ = 2. Определите бюджет (ценность имеющихся благ) 1-го потребителя после обмена.
№ 11. В экономике при совершенной конкуренции производятся два блага по технологиям 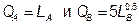 при LA + LB = 500. Функция общественной полезности имеет вид
при LA + LB = 500. Функция общественной полезности имеет вид 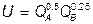 . Если цену блага А принять за 1, то чему должна быть равна цена блага В, чтобы рынок поддерживал в экономике оптимальность по Парето?
. Если цену блага А принять за 1, то чему должна быть равна цена блага В, чтобы рынок поддерживал в экономике оптимальность по Парето?
№ 12. В экономике при совершенной конкуренции производятся два блага по технологиям, представленным производственными функциями короткого периода: 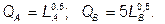 Из общего количества трудовых ресурсов L = 100 в данный момент в производстве блага А используется 80 ед., а в производстве блага В – 20 ед. труда. Какое количество труда перейдет из одной отрасли в другую, если потребительские предпочтения отображаются функцией полезности
Из общего количества трудовых ресурсов L = 100 в данный момент в производстве блага А используется 80 ед., а в производстве блага В – 20 ед. труда. Какое количество труда перейдет из одной отрасли в другую, если потребительские предпочтения отображаются функцией полезности 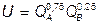 ?
?
№ 13. В экономике при совершенной конкуренции производятся два блага по технологиям, представленным производственными функциями короткого периода: 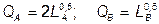 . Из общего количества трудовых ресурсов L = 500 в данный момент в производстве блага А используется 176 ед., а в производстве блага В – 324 ед. труда. На сколько единиц изменится объем выпуска блага В, если потребительские предпочтения отображаются функцией полезности
. Из общего количества трудовых ресурсов L = 500 в данный момент в производстве блага А используется 176 ед., а в производстве блага В – 324 ед. труда. На сколько единиц изменится объем выпуска блага В, если потребительские предпочтения отображаются функцией полезности 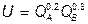 ?
?
№ 14. Для производства двух благ А и В имеется 240 ед. труда и 160 ед. капитала. Технологии производства представлены функциями 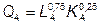 ;
; 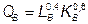 . При производстве блага А используется 16 ед. капитала, а при производстве блага В – 144 ед. Сколько ед. труда должно быть в отрасли А, чтобы обеспечить эффективность по Парето в производстве?
. При производстве блага А используется 16 ед. капитала, а при производстве блага В – 144 ед. Сколько ед. труда должно быть в отрасли А, чтобы обеспечить эффективность по Парето в производстве?
№ 15. Для производства двух благ А и В имеется 300 ед труда и 100 ед капитала Технологии производства представлены функциями:
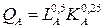
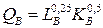
Рабочие распределились между отраслями поровну. Сколько капитала должно быть в отраслях А и В, чтобы обеспечить эффективность по Парето в производстве?
№ 16. Кривая производственных возможностей описывается уравнением 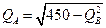 , а функция общественной полезности U = QAQB. Определить оптимальный объем производства товара А.
, а функция общественной полезности U = QAQB. Определить оптимальный объем производства товара А.
№ 17. Кривая производственных возможностей описывается уравнением 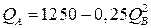 , а функция общественной полезности
, а функция общественной полезности 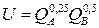 . Определить оптимальный объем производства товара А.
. Определить оптимальный объем производства товара А.
№ 18. Кривая производственных возможностей описывается уравнением 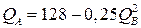 , а функция общественной полезности
, а функция общественной полезности 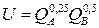 . Определить оптимальный объем производства товара В.
. Определить оптимальный объем производства товара В.
№ 19. В хозяйстве, состоящем из двух отраслей, спрос и предложение представлены следующими функциями:
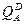 =32-3
=32-3 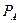 +2
+2 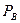
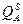 =- 10+ 2
=- 10+ 2 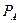 –
– 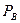
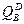 =43-2
=43-2 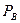 +
+ 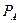
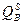 = - 5+
= - 5+ 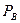 - 0,5
- 0,5 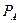
1. При каких ценах на обоих рынках одновременно устанавливается равновесие?
2. Является ли оно устойчивым и почему?
№ 20. На двух взаимосвязанных рынках спрос и предложение отображаются следующими функциями:
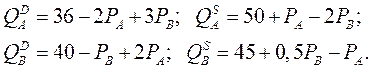
1. При каких ценах на обоих рынках одновременно устанавливается равновесие?
2. Является ли равновесие устойчивым?
№ 21. При существовании двух изолированных рынков спрос и предложение на них отображался соответственно функциями:
QDA = 64 – 4 PA; QSA = – 20 + 2 PA;
QDB = 56 – 3 PB; QSB = – 10 + 3 PB.
Когда оба товара стали продаваться в одном и том же месте, то функции спроса и предложения приобрели следующий вид:
QDA = 64 – 4 PA + 2 PB; QSA = – 20 + 2 PA – PB;
QDB = 56 – 3 PB + PA; QSB = – 10 + 3 PB – 2 PA.
Насколько ден. ед. повысилась цена на товар А?
№ 22. Опрос показал, что готовность жильцов трех домов платить за озеленение их общего двора выражается следующими функциями: P1 = 20 – Q; P2 = 30 – Q; P3 = 40 – Q, где Pi – максимальная сумма денег, которую согласны заплатить жильцы i -го дома за Q -е дерево; Q – количество посаженных деревьев. Общие затраты на озеленение определяются по формуле TC = 0,125 Q 2. Определите:
а) оптимальное число деревьев во дворе трех домов;
б) оптимальную сумму затрат на посадку 1-го дерева.
№ 23. Общество состоит из трех индивидуумов: A, B и C. Функции индивидуального спроса на некоторое общественное благо имеют вид: QА = 80 – P, QВ = 70 – P, QС = 30 – P. Предельные затраты на производство общественного блага постоянны (не зависят от объема производства) и равны 120 ден. ед. на каждую единицу.
а) Определить Парето-оптимальный объем производства общественного блага.
б) Если это общественное благо продавать потребителям по индивидуальным ценам, то какими они должны быть?
в) Допустим, производство общественного блага финансирует правительство за счет налогов. Каждый индивидуум платит налог в размере 40 ден. ед. за каждую единицу общественного блага. На голосование поставлен вопрос об увеличении производства общественного блага сверх Парето-оптимального объема на 5 единиц. Какими будут итоги голосования?
г) Определить равновесный объем производства общественного блага в результате прямого голосования по принципу большинства
№ 24. Готовность абитуриентов платить за учебу в вузах выражается функцией P = 50 – 0,5 N, где Р – сумма платы; N – число абитуриентов, тыс. чел. Выраженная в деньгах предельная общественная полезность (внешняя выгода) высшего образования отображается функцией MU = 70 – 0,5 N, где MU – предельная общественная полезность. Общие затраты вузов на подготовку специалистов заданы функцией TC = 10 N + N 2. Определите:
а) величину внешнего эффекта подготовки одного специалиста с высшим образованием;
б) число студентов, соответствующее максимуму общественной полезности.
№ 25. Рассматривается возможность постройки автомобильного моста через реку. Предполагается, что ежемесячные затраты на содержание моста (включая амортизацию и нормальную прибыль на вложенный капитал) составят 300000 ден. ед. Если установить плату за проезд, то ее величина будет оказывать влияние на число желающих использовать мост. Предполагается, что функция спроса на использование моста имеет вид: Q = 20000 – 500P, где Q – число поездок через мост в течение месяца, P – плата за одну поездку через мост (в ден. ед.).
а) Определить, оправдано ли строительство моста с точки зрения экономической эффективности.
б) Будет ли осуществлять и финансировать данный проект какая-нибудь частная фирма?
№26. Функция затрат завода по производству удобрений имеет вид: TC1 = 20 + 20Q1 + 0,5Q12. Удобрения можно продавать по цене P1 = 30. Затраты птицефермы, использующей то же озеро, что и завод, имеют вид: TC2 = 4 + 5Q2 + 0,4Q22 + Q12. Они растут с увеличением выпуска удобрений. Птицеферма может продавать продукцию по цене P2 = 85. Оба предприятия стремятся к максимизации прибыли.
а) Определить объем выпуска и прибыль каждого предприятия, если озеро – бесплатное общественное благо.
б) Птицеферма приобрела право взимать фиксированную плату с завода за каждую единицу выпуска. Какая плата будет установлена и каковы будут объемы выпуска и прибыль у фермы и завода?
в) Завод по производству удобрений приобрел право на загрязнение озера в необходимых для него размерах. Какую фиксированную плату птицеферма сможет предложить заводу за каждую единицу уменьшения выпуска? Каковы будут объемы выпуска и величина прибыли?
г) Что произойдет, если завод и птицеферма объединятся в единый комбинат?
№ 27. Спрос на жевательную резинку отображается функцией
QD = 200 – 2 P. Общие затраты фирм на ее выпуск соответствуют функции
TCn = 4 Q + 0,5 Q 2, а зависимость затрат на уборку тротуаров от количества купленных резинок выражается функцией TCu = 0,25 Q 2. На сколько выпуск жевательной резинки превышает общественный оптимум, когда расходы на уборку мусора финансирует муниципалитет?
№ 28. В одном из двух соседних фермерских хозяйств выращивают кроликов, а в другом – капусту. Затраты на выращивание кроликов отображаются функцией: ТС1 = 8Q1 + 0.2Q12 - 0.05Q22, где Q1 – количество кроликов, Q2 – количество капусты. Функция затрат на выращивание капусты: ТС2 = 10Q2 + 0.3Q22 + 0,05Q12. Оба фермера стремятся максимизировать свою прибыль и могут продавать любое количество продукции по неизменным ценам Р1 = 28; Р2 = 15. Насколько количество выращенных в этих условиях кроликов превышает общественно оптимальное их количество?
№ 29. Одно из двух соседних фермерских хозяйств выращивает яблоки, а другое занято пчеловодством с целью получения меда. Пчеловодство создает для производства яблок положительный внешний эффект посредством опыления яблонь, а производство яблок для производства меда – отрицательный внешний эффект из-за применения химикатов. Поэтому затраты на выращивание яблок отображаются функцией: ТС1 = 10Q1 + 0.25Q12 - 0.15Q22, где Q1 – количество яблок, Q2 – количество меда. Функция затрат на производство меда: ТС2 = 10Q2 + 0.2Q22 + 0,05Q12. Оба фермера стремятся максимизировать свою прибыль и могут продавать любое количество своей продукции по неизменным ценам Р1 = 40; Р2 = 38. Насколько количество произведенного в этих условиях меда меньше общественно оптимального его количества?
 2015-01-30
2015-01-30 24394
24394








