2015-01-30
273
Рассмотрим различные случаи нахождения 1-ого базисного решения. Ограничения имеют вид неравенств:
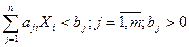
чтобы перейти к равенствам введем дополнительные переменные:
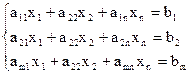(2)
Матрицы дополнительных переменных образуют диагональную первую подматрицу, элементы которой положительны, дополнительные переменные положительны и могут быть использованы для определения 1-ого Б.Р., которые имеют вид: Хn+j=bj, j=1,m. Свободные переменные: Хi=0 i=1,n. Это решение является дополнительным, т.к оно содержит m-положительных компонентов, остальные m-компоненты =0
2) 
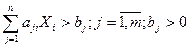
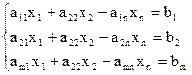(4)
Для этого выберем из системы уравнений (1) у которого правая часть max bj>bk, выберем уравнение у которого bj максимальное, остальные умножаем на (-1) и складываем каждое из них с выбранным уравнением у которого b максимальное (bk=bm), тогда получим новую систему, состоящую из m-1 уравнений эквивалентных исходной но с положительным коэффициентом единичной подматрицы.
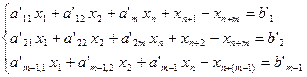(5)
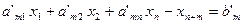(6)
Где a’ji=-aj2+ami,b’j=bm-bj, i=1,n; j=1,m-1(7)
Новая система имеет единичную подматрицу с положительными элементами (порядок матрицы m-1), для того чтобы дополнить эту подматрицу до подматрицы порядка m введем в уравнение (6) искусственную переменную (Хn+m+1) со знаком «+» в результате получим:
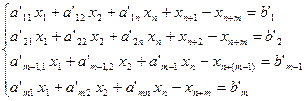(8)
Тогда переменные Хj,i=n+1,n+(m-1), совпадая с (Хn+m+1) образуют единичную подматрицу с положительными элементами, которую использую для нахождения первого базисного решения Хj ≥0, однако при достижении оптимума новая переменная (Хn+m+1)=0. Чтобы исключить базисный вектор, составляющий эту переменную, её вводят в критерий R в след виде:
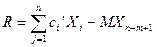, где М- большое положительное число (если ищем максимум)
Значение М должно превышать на много значение R, которое ожидается при решении задачи
3) 
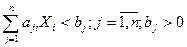
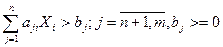
Представляет собой простую комбинацию одного из случаев для неравенства 1-ого вида как в случай 1), а для неравенства 2-вида как в случае 2).
