Прямоугольная (схемы 0 – 5)или круглая (схемы 6 – 9) пластина радиусом
R = 60 см вращается вокруг неподвижной оси с постоянной угловой скоростью ω, заданной в табл. 7. (при знаке «минус» направление ω противоположно показанному на схеме). Ось вращения (схемы 0 – 3 и 8 – 9) перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); в других случаях (схемы 4 – 7) ось вращения OO1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (схемы 0 – 5) или по окружности радиуса R, т.е. по ободу пластины (схемы 6 – 9), движется точка М. Закон ее относительного движения, описываемый уравнением s = AM = f(t) (s – в сантиметрах, t – в секундах), задан в
табл. 7.5. На всех рисунках точка М показана в положении, при котором s = AM > 0 (при s < 0 точка M находится по другую сторону от точки А).
Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 1 с.
Указания. Это задача на сложное движение точки. При ее решении движение точки по пластине считать относительным, а вращательное движение самой пластины – переносным и воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить расчеты, следует изобразить точку М на пластине в том положении, в котором нужно определить ее абсолютную скорость (или ускорение), а не в произвольном положении, показанном на рисунках к задаче.
При решении задач (схемы 6 – 9) не подставлять числового значения R, пока не будут определены положение точки М в момент времени t1 = 1 с и угол между радиусами СМ и СА в этот момент.
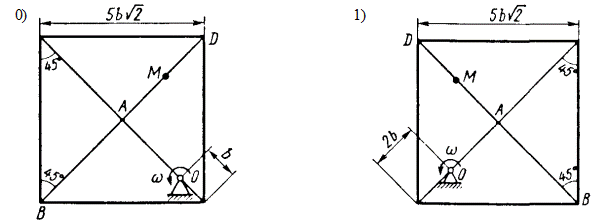
Варианты схем к задаче 3
 |
Таблица 7.5
| Номер варианта условий | ω, 1/с | Схемы 0 – 5 | Схемы 6 – 9 | ||
| b, см | s = AM = f(t) | l | s = AM = f(r) | ||
| -2 | 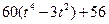 | R | 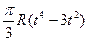 | ||
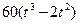 | R | 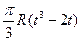 | |||
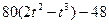 | R | 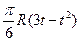 | |||
| -4 | 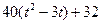 | 3/4 R | 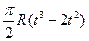 | ||
| -3 | 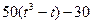 | R | 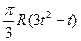 | ||
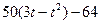 | R | 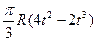 | |||
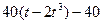 | 4/3 R | 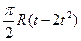 | |||
| -5 | 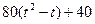 | R | 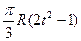 | ||
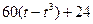 | R | 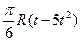 | |||
| -5 | 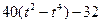 | 4/3 R | 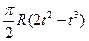 |
 2015-01-30
2015-01-30 2732
2732








