Рассмотрим движение точки М как сложное, считая ее движение по дуге 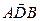 относительным (
относительным (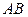 – относительная траектория точки), а вращение шара – переносным движением. Тогда абсолютная скорость (vабс) и абсолютное ускорение (аабс) точки найдутся по формулам:
– относительная траектория точки), а вращение шара – переносным движением. Тогда абсолютная скорость (vабс) и абсолютное ускорение (аабс) точки найдутся по формулам:
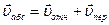 ,
, 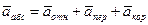 , (1)
, (1)
где,в свою очередь,
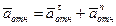
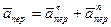 .
.
1. Определим абсолютную скорость точки (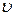 абс)
абс)
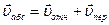 .
.
Относительное движение. Это движение происходит по закону:
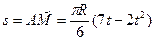 (2)
(2)
Сначала установим, где будет находиться точка М на дуге ADB в момент времени t1. Полагая в уравнении (2) t = 1 с, получим 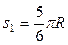 . Toгда
. Toгда 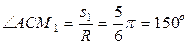 или
или 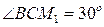 . Изображаем на рис. 7.5,а точку в положении, определяемом этим углом (точка М1). Тогда
. Изображаем на рис. 7.5,а точку в положении, определяемом этим углом (точка М1). Тогда
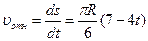 .
.
Для момента времени t1 = 1 с, учитывая, что R = 0,5 м, получим:
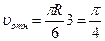 м/с; (3)
м/с; (3)
Знаки показывают, что вектор 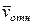 направлен в сторону положительного отсчета расстояния.Для наглядности приведен рис. 7.5,б, где дуга ADB совмещена с плоскостью чертежа.
направлен в сторону положительного отсчета расстояния.Для наглядности приведен рис. 7.5,б, где дуга ADB совмещена с плоскостью чертежа.
Переносное движение. Это движение (вращение) происходит по закону: 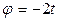 . Найдем угловую скорость (ω) и угловое ускорение (ε) переносного вращения::
. Найдем угловую скорость (ω) и угловое ускорение (ε) переносного вращения:: 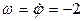 ;
; 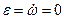 (шар вращается равномерно). Таким образом,
(шар вращается равномерно). Таким образом,
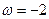 с-1;
с-1; 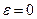 . (4)
. (4)
Знак указывает, что направление противоположно положительному направлению отсчета угла 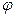 ; отметим это на рис. 7.5,а соответствующей дугой со стрелкой.
; отметим это на рис. 7.5,а соответствующей дугой со стрелкой.
Для определения 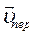 найдем сначала расстояние h точки М1, от оси вращения:
найдем сначала расстояние h точки М1, от оси вращения:
h = R sin 30° = 0,25 м.
Тогда в момент времени t1 = 1 с, учитывая равенства (4), получим:
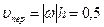 м/с,
м/с,
Изображаем на рис. 7.5,а вектор 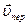 с учетом направления ω.
с учетом направления ω.
Теперь можно вычислить значения 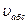 .
.
Так как 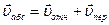 , а векторы
, а векторы 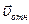 и
и 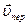 взаимно перпендикулярны (см. рис. 7.5,б), то в момент времени t1 = 1 с:
взаимно перпендикулярны (см. рис. 7.5,б), то в момент времени t1 = 1 с:
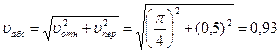 м/с.
м/с.
2. Определим абсолютное ускорение 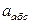 (равенство 1)
(равенство 1)
По теореме о сложении ускорений, так как 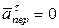 ,
,
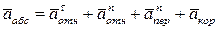 (5)
(5)
Теперь находим числовые значения 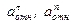 :
:
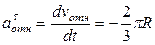 ;
; 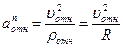 ,
,
где 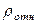 – радиус кривизны относительной траектории, т.е. дуги ADB.
– радиус кривизны относительной траектории, т.е. дуги ADB.
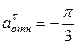 м/с2;
м/с2; 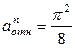 м/с2.
м/с2.
Вектор 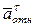 – лежит на одной прямой с вектором
– лежит на одной прямой с вектором 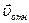 и направлен в противоположную сторону; вектор
и направлен в противоположную сторону; вектор 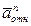 направлен к центру С дуги ADB. Изображаем все эти векторы на рис. 7.5, а.
направлен к центру С дуги ADB. Изображаем все эти векторы на рис. 7.5, а.
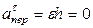 ,
, 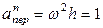 м/с2. (6)
м/с2. (6)
Вектор 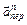 - направлен к оси вращения.
- направлен к оси вращения.
Кориолисово ускорение. Так как угол между вектором 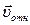 и осью вращения (вектором
и осью вращения (вектором 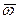 ) равен 60°, то численно в момент времени t1 = 1 с (см. равенства (3) и (4))
) равен 60°, то численно в момент времени t1 = 1 с (см. равенства (3) и (4))
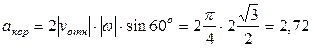 м/с2. (7)
м/с2. (7)
Направление 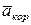 найдем, спроектировав вектор
найдем, спроектировав вектор 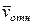 на плоскость, перпендикулярную оси вращения (проекция направлена так же, как вектор
на плоскость, перпендикулярную оси вращения (проекция направлена так же, как вектор 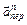 ), и повернув затем эту проекцию в сторону ω, т.е. по ходу часовой стрелки, на 90°. Иначе направление
), и повернув затем эту проекцию в сторону ω, т.е. по ходу часовой стрелки, на 90°. Иначе направление 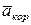 можно найти, учтя, что
можно найти, учтя, что 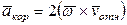 . Изображаем вектор
. Изображаем вектор 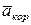 на рис. 7.5,а.
на рис. 7.5,а.
и 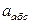 .
.
Для определения 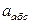 проведем координатные оси M1xyz (рис. 7.5,а) и вычислим проекции вектора
проведем координатные оси M1xyz (рис. 7.5,а) и вычислим проекции вектора 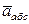 на эти оси. Учтем при этом, что вектор
на эти оси. Учтем при этом, что вектор 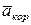 лежит на проведенной оси х, а векторы
лежит на проведенной оси х, а векторы 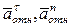 и
и 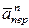 расположены в плоскости дуги ADB, т.е. в плоскости M1yz (рис. 7.5,б). Тогда, проектируя обе части равенства (7) на координатные оси и учтя одновременно равенства (3), (5), (6), получим для момента времени t1 = 1с:
расположены в плоскости дуги ADB, т.е. в плоскости M1yz (рис. 7.5,б). Тогда, проектируя обе части равенства (7) на координатные оси и учтя одновременно равенства (3), (5), (6), получим для момента времени t1 = 1с:
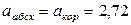 м/с2,
м/с2,
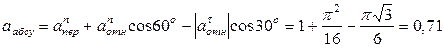 м/с2,
м/с2,
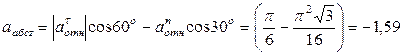 м/с2.
м/с2.
Отсюда находим значение 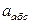 в момент времени t1 = 1с:
в момент времени t1 = 1с:
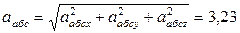 м/с2.
м/с2.
Ответ 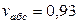 м/с;
м/с; 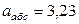 м/с2.
м/с2.
 2015-01-30
2015-01-30 1403
1403
