| Правило условного силлогизма | Правило modus tollens | Правило отрицания дизъюнкции (ОД) | Правило отрицания конъюнкции (ОК) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Правило контрапозиции 1 | Правило контрапозиции 2 | Правило сложной контрапозиции | Правило простой конструктивной дилеммы (П.К.Д.) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| Правило сложной конструктивной дилеммы (С.К.Д.) | Правило простой деструктивной дилеммы (П.Д.Д.) | Правило сложной деструктивной дилеммы (С.Д.Д.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Правило условного силлогизма
| Правило | Доказательство | ||
| А→ В | А→ В | 1. | …………… |
| В → С | В →С | 2. | …………… |
| А→ С | А | 3. | …………… |
| В | 4. | …………… | |
| С | 5. | …………… | |
| А→ С | 6. | …………… |
Правило modus tollens
| Правило | Доказательство правила: | ||
| А → В | А → В | …………… | |
| В | В | …………… | |
| А | А | …………… | |
| В | …………… | ||
| А | …………… |
Правило отрицания дизъюнкции (ОД)
| Правило | Доказательство: | ||
| (А∨В) | (А∨В) | …………… | |
| А∧В | А | …………… | |
| А∨В | …………… | ||
| А | …………… | ||
| В | …………… | ||
| А∨В | …………… | ||
| В | …………… | ||
| А∧В | …………… |
Правило отрицания конъюнкции (ОК)
| Правило | Доказательство: | ||
| (А∧В) | (А∧В) | …………… | |
| А∨В | (А∨В) | …………… | |
| А∧В | …………… | ||
| А | …………… | ||
| А | …………… | ||
| В | …………… | ||
| В | …………… | ||
| А∧В | …………… | ||
| (А∨В) | …………… | ||
| А∨В | …………… |
Правило контрапозиции 1
| Правила контрапозиции: | Доказательство | ||
| А → В | А → В | …………… | |
| В→А | В | …………… | |
| А | …………… | ||
| В→А | …………… |
Правило контрапозиции 2
| 2 Правило | Доказательство | ||
| В→А | В→А | …………… | |
| А → В | А | …………… | |
| А | …………… | ||
| В | …………… | ||
| В | …………… | ||
| А → В | …………… |
Правило сложной контрапозиции
| Правило: | Доказательство: | ||
| (А∧В)→С | (А∧В)→С | …………… | |
| (А∧С)→В | А∧С | …………… | |
| А | …………… | ||
| С | …………… | ||
| (А∧В) | …………… | ||
| А∨В | …………… | ||
| А | …………… | ||
| В | …………… | ||
| (А∧С)→В | …………… |
Правило простой конструктивной дилеммы (П.К.Д.)
| Правило | Доказательство: | ||
| А→С | А→С | …………… | |
| В →С | В →С | …………… | |
| А∨В | А∨В | …………… | |
| С | С | …………… | |
| А | …………… | ||
| B | …………… | ||
| B | …………… | ||
| С | …………… |
Правило сложной конструктивной дилеммы (С.К.Д.)
| Правило | Доказательство: | ||
| А→В | А→В | …………… | |
| С→D | С→D | …………… | |
| А∨C | А∨C | …………… | |
| В ∨D | A | …………… | |
| В | …………… | ||
| В∨D | …………… | ||
| A →(В∨D) | …………… | ||
| С | …………… | ||
| D | …………… | ||
| B∨D | …………… | ||
| С →(B∨D) | …………… | ||
| B∨D | …………… |
Правило простой деструктивной дилеммы (П.Д.Д.)
| Правило | Доказательство: | ||
| А→В | А→В | …………… | |
| А→С | А→С | …………… | |
| В ∨С | В ∨С | …………… | |
| А | В→А | …………… | |
| С→А | …………… | ||
| А | …………… |
Правило сложной деструктивной дилеммы (С.Д.Д.)
| Правило | Доказательство: | ||
| А→В | А→В | …………… | |
| С→D | С→D | …………… | |
| В ∨D | В∨D | …………… | |
| А ∨С | В→А | …………… | |
| D→С | …………… | ||
| А∨С | …………… |
Упражнение
Список названий правил вывода
1. ВК: 2. ВД1: 3. УД2: 4. УИ2: 5. УЭ1: 6. 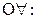 7.
7. 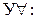 8.
8. 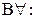 9. УК1: 10. ВД2: 11. ОД: 12. ОИ: 13. УЭ2: 14.
9. УК1: 10. ВД2: 11. ОД: 12. ОИ: 13. УЭ2: 14. 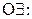 15.
15. 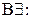 16.
16. 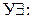 17. УК2: 18. УД1: 19. УИ1: 20. ВЭ: 21. ВО: 22. ОК: 23. УО:
17. УК2: 18. УД1: 19. УИ1: 20. ВЭ: 21. ВО: 22. ОК: 23. УО:
Список схем правил вывода
1. 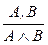 ; 2.
; 2. 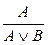 ; 3.
; 3. 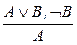 ; 4.
; 4. 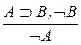 ; 5.
; 5. 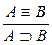 ; 6.
; 6. 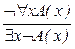 ; 7.
; 7. 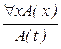 ; 8.
; 8. 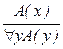 ; 9.
; 9. 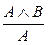 ; 10.
; 10. 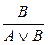 ; 11.
; 11. 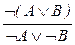 ; 12.
; 12. 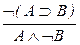 ; 13.
; 13. 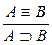 ; 14.
; 14. 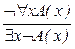 ; 15.
; 15. 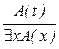 ; 16.
; 16. 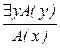 ; 17.
; 17. 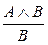 ; 18.
; 18. 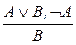 ; 19.
; 19. 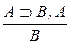 ; 20.
; 20. 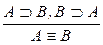 ; 21.
; 21. 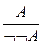 ; 22.
; 22. 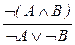 ; 23.
; 23. 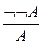 ;
;
Список схем правил вывода с пропущенным выводом
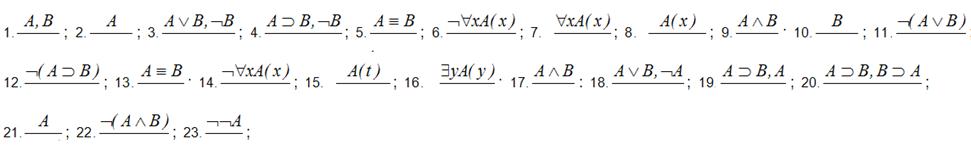
где А(t) – результат правильной подстановки термина t вместо x в А(х);
где А(х) – результат правильной подстановки переменной х вместо y в А(y);
x, a1, a2,…, an отмечены, причем переменная x безотносительно отмечена, а переменные a1, a2,…, an отмечены относительно x.
Пояснения
1. Буквами A и В при формулировке правил обозначаются формулы. Выражение А(у) обозначает формулу, имеющую свободное вхождение переменной у, a A(t) — формулу, имеющую вхождение терма t, причем если t — переменная, то A(t) — формула, имеющая свободное вхождение этой переменной, а если t — индивидная константа, то A(t) — формула, содержащая эту константу.
2. Названия правил вывода расшифровываются так: ВК — введение конъюнкции, УК — удаление конъюнкции, OK — отрицание конъюнкции, ВД — введение дизъюнкции, УД — удаление дизъюнкции, ОД — отрицание дизъюнкции, УИ — удаление импликации, ОИ — отрицание импликации, ВЭ — введение эквивалентности, УЭ — удаление эквивалентности, ВО — введение (двойного) отрицания, УО — удаление (двойного) отрицания, 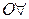 — отрицание квантора общности,
— отрицание квантора общности, 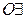 — отрицание квантора существования,
— отрицание квантора существования, 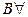 — введение квантора общности,
— введение квантора общности, 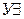 — удаление квантора существования,
— удаление квантора существования, 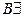 — введение квантора существования,
— введение квантора существования, 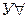 — удаление квантора общности.
— удаление квантора общности.
 2015-01-30
2015-01-30 267
267








