Пример. Пусть требуется обосновать выводимость. Ход обоснования: (1)

Пусть требуется обосновать выводимость
.
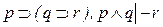Ход обоснования:
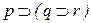
(1)	- гипотеза
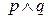
(2)	- гипотеза;
(3) p	– из (2) по УК1;
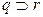
(4)	- из (1), (3) по УИ1;
(5) q	– из (2) по УК2;
(6) r	– из (4), (5) по УИ1.

Таким образом, 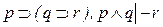по определению вывода на основе (1)-(6).

Пример. Докажем, что из гипотез 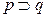, , 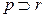p выводима формула q.

Ход доказательства:
(1) 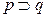;	- гипотеза
(2) p;	- гипотеза
(3) q	– из (1), (2) по УИ1.

Таким образом, 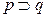, , 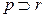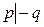по определению вывода на основе (1)-(3).

	ВК:	;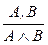
	ВД1:	;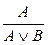
	УД2:	;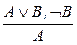
	УИ2:	;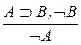
	УЭ1:	;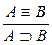
		;
		;
		;
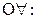
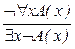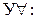
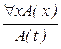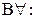
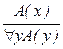	УК1:	;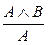
	ВД2:	;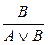
	ОД:	;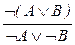
	ОИ:	;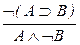
	УЭ2:	;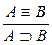
		;
		;
		;
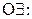
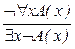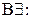
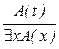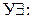
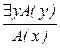	УК2:	;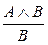
	УД1:	;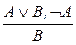
	УИ1:	;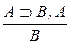
	ВЭ:	;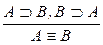
	ВО:	;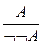
	ОК:	;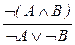
	УО:	;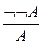

Правила вывода второго рода:

ПД: ;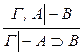
СА: .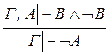
ДОП: ;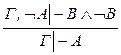

100.