Пусть требуется обосновать выводимость
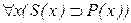 ,
, 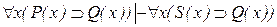 .
.
| Ход доказательства: | |
+ (1) 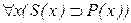 ; ;
| Гипотеза |
+(2) 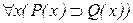 ; ;
| Гипотеза |
+ (3) 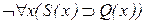 ; ;
| Гипотеза |
(4) 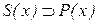
| из (1) по 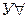 ; ;
|
(5) 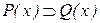
| из (2) по 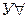 ; ;
|
(6) 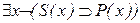
| из (3) по 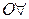 ; ;
|
(7) 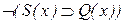
| из (6) по 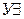 ; x отмечена; ; x отмечена;
|
(8) 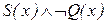
| из (7) по 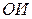 ; ;
|
(9) 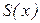
| из (8) по 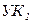 ; ;
|
(10) 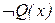
| из (8) по 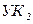 ; ;
|
(11) 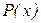
| из (4), (9) по 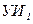 ; ;
|
(12) 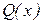
| из (5), (11) по 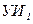 ; ;
|
(13) 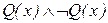
| из (10), (12) по 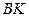 . .
|
Таким образом:
1. 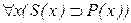 ,
, 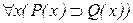 ,
, 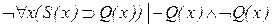 по определению вывода на основе (1)-(13); х отмечена (выводимость обоснована не полностью, т.к. безотносительность отмеченная переменная имеет свободное вхождение
по определению вывода на основе (1)-(13); х отмечена (выводимость обоснована не полностью, т.к. безотносительность отмеченная переменная имеет свободное вхождение
Пусть переменная
А означает высказывание «Я сдам экзамен по логике»,
В- «Декан доволен мной»,
С – «Мама накормит меня прекрасным ужином»,
D - «На меня обратят внимание девушки»,
E – «Любимая футбольная команда выиграла матч».
(A É (B É C))
├ (B É (A É C))
Переведите на естественный язык следующие формулы логики высказываний.
Если Я СДАМ ЭКЗАМЕН ПО ЛОГИКЕ, и, если ДЕКАН будет ДОВОЛЕН МНОЙ, то МАМА НАКОРМИТ МЕНЯ ПРЕКРАСНЫМ УЖИНОМ
├Если ДЕКАН оказался ДОВОЛЕН МНОй и если Я СДАЛ ЭКЗАМЕН ПО ЛОГИКЕ, то МАМА НАКОРМИла МЕНЯ ПРЕКРАСНЫМ УЖИНОМ)
Если я сдам экзамен по логике, то мир перевернется, или если мир перевернется, то я сдам экзамен по логике»
= (A É B) Ú (B É A)
«Он обязательно полюбит меня, но навряд ли это произойдет, если он узнает о всех моих похождениях».
= А & Ø (B É A)
“Я сдам экзамен по логике, если и только если не буду пропускать занятия и научусь решать задачи»
= A «(Ø B & С)
«Нечто утверждается либо отвергается; третьего не дано»
= (А Ú Ø A)
«Нельзя нечто утверждать и отвергать одновременно»
= Ø (A & Ø A)
Правила введения и удаления дизъюнкции (В.Д.), (У.Д.):
Правила удаления импликации (У.И.):
Правила введения и удаления эквивалентности (В.Э.), (У.Э.):
Правила введения и удаления двойного отрицания (В.О.), (У.О.):
 2015-01-30
2015-01-30 533
533








