Решение краевой задачи методом Фурье

Изложим существо метода Фурье или метода разделения переменных, рассматривая задачу о колебаниях струны с закрепленными концами. Как мы уже знаем, эта задач сводится к решению волнового уравнения

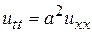(53)

при начальных условиях

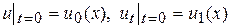(54)

и граничных условиях

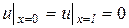. (55)

Будем искать нетривиальные частные решения уравнения (55), удовлетворяющие условиям (52), в виде произведения двух функций, зависящих только от одного аргумента X=X(x) и T=T(t), а именно

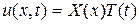, (56)

Вычислив производные 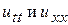от (56) и, подставив их в уравнение (53), получим

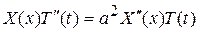(57)

или

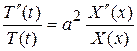. (58)

Равенство (58) выполняется только в том случае, если обе части его не зависят ни от х, ни от t, т.е. представляют собой одну и туже постоянную, которую обозначим за 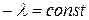, т.е.

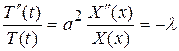. (59)

Отсюда получаем два обыкновенных однородных линейных уравнений второго порядка

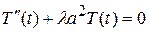(60)

и

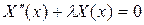. (61)

Для того, чтобы получить не равные нулю решения вида (56), удовлетворяющие граничным условиям (55), необходимо найти нетривиальные решения, удовлетворяющие граничным условиям

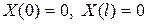. (62)

Таким образом, мы пришли к задаче: найти такие значения параметра l, которые назовем собственными числами или собственными значениями. Нетривиальные решения уравнения (61), которые соответствуют этим собственным значениям, назовем собственными функциями, удовлетворяющие граничным условиям (62). Задачу отыскания собственных значений и собственных функций называют задачей Штурма-Лиувилля.

Рассмотрим три случая задачи (61), (62)

1) l< 0.

В этом случае общее решение уравнения (61) имеет вид

,

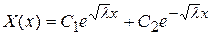удовлетворяя граничным условиям (62), получим

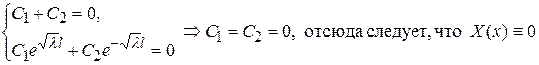
2) l =0.

В этом случае общее решение уравнения (61) имеет вид

,

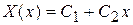удовлетворяя граничным условиям (62), получим

.

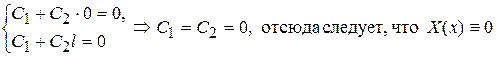3) l >0.

В этом случае общее решение уравнения (61) имеет вид

,

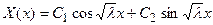удовлетворяя граничным условиям (62), получим

.

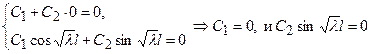В уравнении 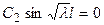постоянная С ₂ не может быть равной нулю, поскольку в этом случае, мы получим тривиальное решение задачи (61), (62) - Х (х) ≡ 0. Поэтому для того, чтобы равенство 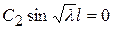выполнялось необходимо, чтобы выполнялось равенство 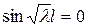, а оно выполняется только тогда, когда 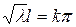(k- любое целое число). Следовательно, нетривиальное решение задачи (61), (62) возможно лишь при собственных значениях l_k равных

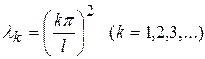. (63)

Только этим собственным значениям соответствуют (нормированные) собственные функции вида

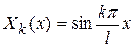, (64)

которые будут являться нетривиальными решениями задачи (61), (62).

Собственные значения (63) подставим в уравнение (60)

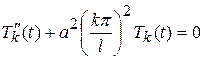. (65)

Общее решение этого уравнения имеет вид

. (66)

Подставляя функции (64) и (66) в (56), найдем

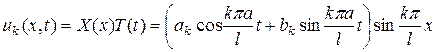, (67)

где a_k и b_k – произвольные постоянные.

Эта функция удовлетворяет уравнению (53) и граничным условиям (55) при любых коэффициентах a_k и b_k. В силу линейности и однородности уравнения (53) всякая конечная сумма решений (67) также будет решением уравнения (53), поэтому можно записать

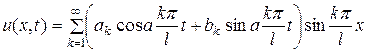. (68)

Определяя постоянные a_k и b_k так, чтобы сумма ряда (68) удовлетворяла и начальным условиям (54), приходим к равенствам

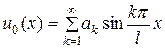(69)

. (70)

Эти формулы (69) и (70) дают разложение функций 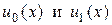в ряд Фурье по синусам в интервале (0, l). Коэффициенты этих разложений вычисляются по известным формулам

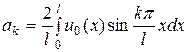, (71)

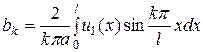. (72)

Таким образом, ряд (68) полностью определяет решение исходной краевой задачи (53)-(55).

Пример 11. Решить краевую задачу для неоднородного уравнения гиперболического типа

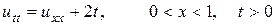, (11.1)

при начальных условиях

(11.2)

и граничных условиях

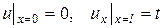. (11.3)

▲ Подберем сначала такую функцию v, чтобы удовлетворяла граничным условиям (11.3). Пусть, например, v = xt. Тогда

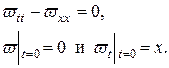
Следовательно, функция определяемая как

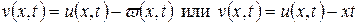(11.4)

удовлетворяет уравнению

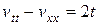(11.5)

однородным граничным условиям

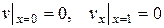(11.6)

и нулевым начальным условиям

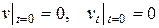. (11.7)

Применим метод Фурье для решения однородного уравнения

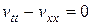
при условиях (11.6), (11.7), для этого положим

.

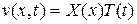В результате приходим к следующей задаче Штурма-Лиувилля:

, .

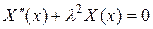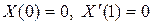Решая эту задачу, находим собственные значения

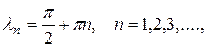
и соответствующие им собственные функции

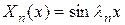. (11.8)

Теперь будем искать решение неоднородного уравнения (11.5) с однородными граничными (11.6) и нулевыми начальными (11.7) условиями в виде следующего ряда

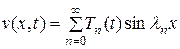, (11.9)

причем

. (11.10)

Подставив 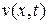из (11.9) в уравнение (11.5), получим

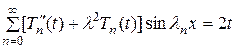. (11.11)

Для нахождения функции T_n(t) разложим единицу в ряд Фурье по системе функций (11.8) на интервале (0,1):

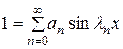. (11.12)

Так как

,

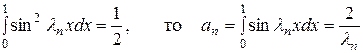и из (11.11) и (11.12) получаем уравнение

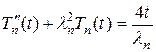, (11.13)

которое является обыкновенным неоднородным линейным уравнением второго порядка. Его общее решение равно сумме общего решения, соответствующего ему однородного уравнения и частного решения неоднородного уравнения (11.13). Общее решение однородного уравнения

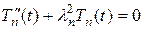
имеет вид

.

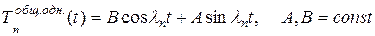Частное решение уравнения (11.13) можно найти, например, методом неопределенных коэффициентов. Сравним вид правой части уравнения (11.13) с выражением

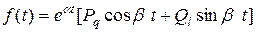(11.14)

и определим значения параметров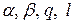

При этих значениях параметров выражение (11.14) имеет вид правой части уравнения (11.13). Следовательно, можно записать частное решение этого уравнения в виде

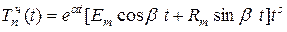. (11.15)

Так как 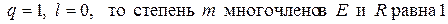, и эти многочлены имеют вид . При наших значениях параметров 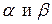комплексное число 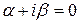равно нулю и не совпадет ни с одним из корней характеристического уравнения 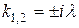, поэтому значение показателя s в формуле (11.15) равно нулю. Таким образом, частное решение через неопределенные коэффициенты имеет вид

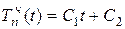. (11.16) Подставив (11.16) в уравнение (11.13), получим

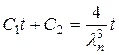. (11.17)

Приравнивая коэффициенты при одинаковых функциях в правой и левой частях уравнения (11.17), найдем значения неопределенных коэффициентов С ₁ и С ₂

.

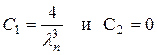Следовательно, частное решение уравнения (11.13) имеет вид

.

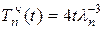Таким образом, общее решение уравнения имеет вид

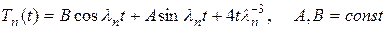. (11.18)

Используя условие (11.10) найдем значения коэффициентов А и В:

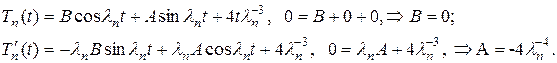
Подставляя полученные коэффициенты А и В в формулу (11.18), получим

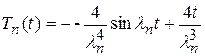. (11.19)

Затем, подставляя (11.19) в решение (11.9) и используя равенство (11.4) окончательно получим решение исходной задачи (11.1) – (11.3):

.▲

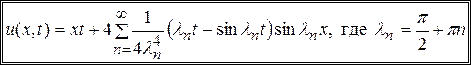Пример 12. Струна, закрепленная на концах x =0 и x=l, имеет в начальный момент форму параболы 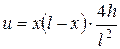. Определить смещение точек струны от оси абсцисс, если начальные скорости отсутствуют (рис.2).

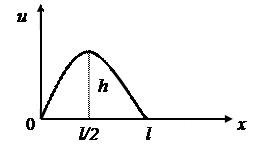
Рис.2.

▲ Запишем начальные условия

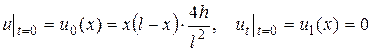(12.1)

и граничные условия

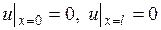. (12.2)

в соответствии с условиями задачи.

Решение исходной задачи дается формулой (60)

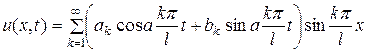, (12.3)

в которой коэффициенты ряда - a_k и b_k, определяются по формулам

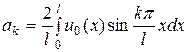, (12.4)

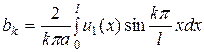. (12.5)

Подставив начальные условия (12.1) в формулы (12.4) и (12.5), найдем значения коэффициентов a_k и b_k

а коэффициент b_k = 0, т.к. .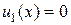

Подставляя найденные значения коэффициентов a_k и b_k, в формулу (12.3), получим

.

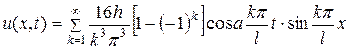При четном k =2 n выражение 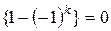, следовательно, и решение 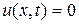, а при нечетном k =2 n +1 выражение 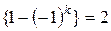, поэтому окончательное решение исходной задачи имеет вид

.▲

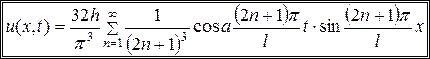Аналогом струны в двумерном пространстве считается мембрана и уравнение ее колебаний имеет вид

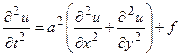. (73)

Волновое уравнение также описывает крутильные колебания стержней, плоские акустические волны в жидкостях и газах, плоские электромагнитные волны в непроводящих средах и т.п.