Уравнение теплопроводности и постановка краевых задач

Уравнения параболического типа наиболее часто встречаются при изучении процессов теплопроводности и диффузии. Уравнение теплопроводности было получено при решении задачи о распространении тепла в неком стержне с плотностью r (x), удельной теплоемкостью с (x) и коэффициентом внутренней теплопроводности k. Вывод этого уравнения базируется на законе Фурье, согласно которому количество тепла, проходящее за время ∆ t через малую площадку ∆ S, лежащую внутри рассматриваемого тела, определяется формулой

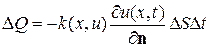, (74)

где n – нормаль к площадке, направленная в сторону передачи тепла, k (x,u) - коэффициент внутренней теплопроводности, u (x,t) – температура тела в точке 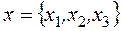в момент времени t.

Предположим, что тело изотропно в отношении теплопроводности. Тогда k (x,u) не зависит от направления площадки. Для вывода уравнения, которому удовлетворяет температура u (x,t), выделим внутри тела объем W, ограниченный поверхностью S. Согласно закону Фурье количество тепла, втекающего в W через поверхность S за промежуток времени [ t ₁, t ₂], равно

.

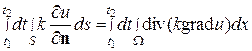Если F (x,t) – плотность тепловых источников, то количество тепла, образованное за их счет в W за указанный промежуток времени равно

.

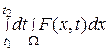Общее количество притекшего в W за время от t ₁ до t ₂ тепла можно подсчитать также и через приращение температуры:

,

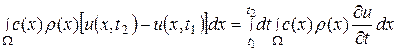следовательно, можно записать

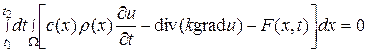, (75)

(при этом предполагается, что подинтегральная функция непрерывна). В силу произвольности W и промежутка времени [ t ₁, t ₂] из выражения (75) вытекает равенство

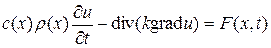, (76)

т.к. 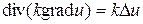, где ∆ - оператор Лапласа, то уравнение (76) можно записать в виде

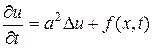, (77)

где .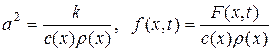

Уравнение (76) или (77) называются уравнением теплопроводности. Для одномерного случая при f (x,t) = 0 оно имеет вид

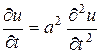. (78)

Для выделения единственного решения уравнения теплопроводности необходимо к этому уравнению присоединить начальные и граничные условия.

Для одномерного процесса распределения температуры, описываемого уравнением (78) начальное условие имеет вид

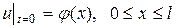, (79)

где 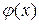- заданная функция.

Кроме того, для того, чтобы узнать тепловой режим на поверхности тела S, необходимо задать граничные условия.

В задачах теплопроводности граничные условия могут быть заданы различными способами, например:

1) поверхности тела задают температуру

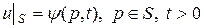, (80)

где 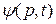- известная функция точки р поверхности S и времени t.

Условие (80) называют граничным условием 1-го рода.

2) в каждой точке на поверхности тела задают тепловой поток

,

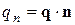где 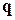- вектор плотности теплового потока; 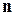- единичная внешняя нормаль к поверхности тела S. По закону Фурье 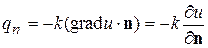, следовательно, граничное условие в этом случае имеет вид

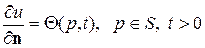, (81)

где 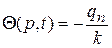- известная функция точки р поверхности S и времени t.

Условие (81) называют граничным условием 2-го рода и оно задает на поверхности S нормальную производную температуры.

В случае теплоизолированной поверхности 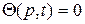на всей поверхности S мы имеем однородное условие

.

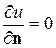3) Граничное условие 3-го рода описывает тепловой режим на поверхности тела и задает связь между температурой u и ее нормальной производной 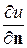в любой точке поверхности тела

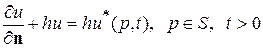, (82)

где 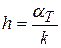; 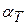- коэффициент теплообмена (теплоотдачи), зависящий от свойств среды, а в общем случае и от разности температур тела и и внешней среды u*.

Формально граничные условия 1-го, 2-го и 3-го рода можно объединить в виде обобщенного граничного условия

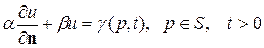, (83)

из которого можно получить все рассмотренные краевые условия.

Пример 13. Задачи о диффузии. Вывести уравнение диффузии вещества в неподвижной среде, занимающей ограниченную область 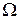с границей Г, если задана плотность источников F(x,t) и диффузия происходит с поглощением (например, частицы диффундирующего вещества вступают в химическую реакцию с веществом среды), причес скорость поглощения в каждой точке пространства 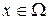пропорциональна плотности 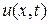диффундирующего вещества.

Получить краевые условия для следующих случаев:

1) на границе области поддерживается заданная плотность;

2) граница непроницаема;

3) граница полупроницаема, причем диффузия через границу происходит по закону, подобному закону Ньютона для конвективного теплообмена.

▲ Вывод уравнения основывается на законе Нэрнста, согласно которому количество вещества, проходящее за малый промежуток времени 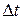через малую площадку 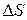, равно

,

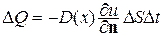где D(x) – коэффициент диффузии, n – нормаль к элементу 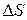, направленная в сторону перемещения вещества. Пусть 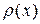- коэффициент плотности среды.

Выделим некоторый объем 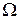с границей S и составим баланс количества вещества, пришедшего в 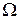за промежуток времени .

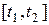Количество вещества, пришедшего в 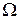через границу S, согласно закону Нэрнста равно

.

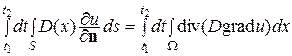Количество вещества, образовавшегося в 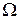за счет источников, равно

.

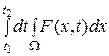Количество вещества в 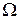уменьшилось на величину

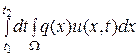
за счет поглощения среды (q(x) – коэффициент поглощения). Поскольку приращение количества вещества в 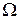за промежуток 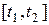равно также

,

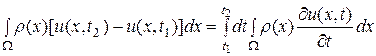то

.

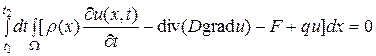В силу произвольности объема 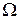и промежутка 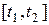из полученного равенства вытекает

.

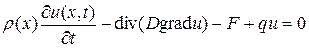Это и есть классическое уравнение диффузии. Из физических соображений ясно, что для однозначного описания процесса диффузии необходимо знать начальное распределение плотности

,

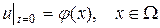и режим диффузии на границе области.

Краевые условия для разных случаев имеют вид:

1) если на границе области поддерживается заданная плотность, то

;

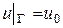2) если граница непроницаема, то

;

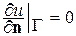3) если граница полупроницаема, то

,

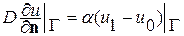где 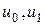-заданные функции; a -коэффициент проницаемости границы Г. ▲