Определение 7. Умножение матрицы 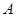 на матрицу
на матрицу 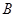 определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц
определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц 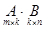 называется матрица
называется матрица 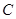 , каждый элемент которой
, каждый элемент которой 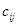 равен сумме произведений элементов
равен сумме произведений элементов 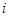 -ой строки матрицы
-ой строки матрицы 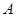 на соответствующие элементы
на соответствующие элементы 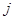 -го столбца матрицы
-го столбца матрицы 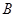 :
:
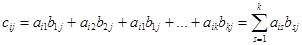 , где
, где 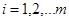 ,
, 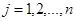 .
.
Пример. Вычислить произведение матриц 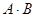 , где
, где
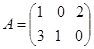 ,
, 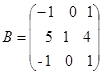 .
.
Решение. Найдем размер матрицы произведения 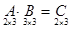 , следовательно, умножение возможно.
, следовательно, умножение возможно.
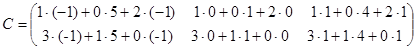 =
= 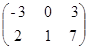 .
.
Определение 8. Матрица 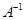 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице 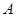 , если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
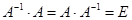 .
.
 2014-10-30
2014-10-30 607
607








