Как и при работе алгоритма ТHAID, задается номинальный признак-функция Y. Поведение каждого респондента здесь понимается так же, как выше (скажем, это выбор респондентом той или иной позиции при голосовании). А вот групповое поведение будем оценивать по-другому. А именно, будем ассоциировать его не с частотой модального значения признака Y, а со всем распределением этого признака. Как и выше, в нашу задачу, наряду с поиском сочетаний значений рассматриваемых признаков, детерминирующих интересующее нас групповое поведение, входит поиск конкретных видов такого поведения - конкретных распределений значений признака Y, детерминируемых нашей анкетой.
Алгоритм состоит из ряда шагов, сходных с теми, которые были описаны выше. На каждом шаге происходит склеивание определенных градаций каждого признака и выделение той переменной, в соответствии со значениями которой совокупность респондентов делится далее на части.
Рассмотрим принципиальные моменты алгоритма, связанные с пониманием искомых типов поведения респондентов и позволяющие реализовывать упомянутые процедуры.
Определение склеиваемых градаций. Покажем на примере, как определяется, какие градации анализируемого признака Х должны склеиваться.
Пусть Y – электоральное поведение респондента в том же смысле, какой был использован в п. 2.5.3.2, а признак Х – это профессия с градациями “врач”, “учитель”, “рабочий”. Рассмотрим частотную таблицу, связывающую эти два признака (таблица 27).
Таблица 27.
Таблица сопряженности, использованная для определения “склеиваемых” градаций признака “профессия” в процессе использования алгоритма CHAID
| Профессия | Предполагаемое голосование | Итого | ||||
| Е | Ж | З | Л | Я | ||
| Врач | ||||||
| Учитель | ||||||
| Рабочий | ||||||
| Итого |
Склеить мы должны такие градации, которые не имеет смысла рассматривать дальше отдельно из-за того, что респонденты, отметившие одну градацию, обладают тем же электоральным “поведением”, что и респонденты, отметившие другую. Рассмотрение соответствующих совокупностей респондентов отдельно не имеет смысла. Нетрудно видеть, что такими свойствами обладают градации “врач” и “учитель”. Если мы рассмотрим отдельно представителей этих профессий, то уж никак не получим разные типы избирателей: половина врачей хочет голосовать за Я и половина учителей - тоже. Одинаковое количество учителей (5 человек, примерно 17 %) хочет голосовать за Е и З соответственно, и то же самое можно сказать о врачах и т.д. Нетрудно видеть, что сказанное является следствием того, что первые две строки нашей частотной таблицы пропорциональны.
Относительно же врачей и рабочих мы подобные выводы сделать не можем. Вероятно, эти альтернативы нельзя объединять. Напротив, имеет смысл разделить нашу совокупность на две части, рассмотрев врачей и рабочих отдельно. Они являют собой совершенно разный тип электорального поведения: за Я собираются голосовать 50% (30 человек) врачей и менее 2% (2 человека) рабочих и т.д. Ясно, что это – следствие сильного отклонения от пропорциональности первой и третьей строк нашей таблицы.
Вспомним теперь критерий “хи-квадрат”. Пропорциональность строк таблицы сопряженности означает равенство этого критерия нулю и, следовательно, влечет за собой принятие нуль-гипотезы – гипотезы об отсутствии связи между переменными. Отсутствие пропорциональности влечет отвержение нуль-гипотезы, т.е. согласие с наличием связи между переменными. И приведенные выше рассуждения по существу говорят о том, что склеивать надо те альтернативы, которые, будучи “вырванными” из общего списка и рассмотренные отдельно, как значения “вспомогательного” дихотомического признака (в нашем случае - признака с двумя альтернативами: “учитель” и “врач”) приведут нас к выводу об отсутствии связи между этим вспомогательным признаком и Y.
Но эта формулировка не очень корректна, поскольку критерий “хи-квадрат” не “говорит” о том, есть или нет связь между переменными, а лишь дает основание принять или отвергнуть гипотезу об отсутствии связи на определенном уровне значимости a. Поэтому более грамотной будет следующее правило, по которому мы определяем, какие именно две альтернативы рассматриваемого признака надо склеить.
Для конкретного признака Х проверяем все пары альтернатив. Считаем, что каждая пара отвечает своему дихотомическому признаку и, задавшись уровнем значимости (скажем, a = 0,05), вычисляем критерий “хи-квадрат” для этого признака и Y. Отбираем те пары, для которых значение Х2 не превышает соответствующее критическое значение. Ясно, что это пары, для которых имеет смысл принять нашу нуль-гипотезу. Далее выбираем ту пару, для которой Х2 меньше всего, т.е. для которой наша нуль гипотеза принимается как бы с большей надежностью. Именно альтернативы этой пары мы и склеиваем.
Выбор признака для разбиения совокупности. Склеив какие-то альтернативы в каждом из анализируемых признаков, мы вычисляем критерий “хи-квадрат” между каждым из оставшихся к рассматриваемому шагу признаком Хi и Y. Здесь поступим противоположным образом по сравнению с тем, что было выше: отберем те признаки Хi, для которых наш критерий превышает критическое значение, т.е., для которых имеет смысл отвергнуть гипотезу об их независимости от Y, т.е. считать, что между каждым из них и Y есть связь. Среди этих признаков отберем тот, для которого 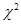 имеет наибольшее значение, т.е. тот, для которого связь существует с наибольшей вероятностью. По его градациям мы и будем далее разбивать совокупность респондентов.
имеет наибольшее значение, т.е. тот, для которого связь существует с наибольшей вероятностью. По его градациям мы и будем далее разбивать совокупность респондентов.
Описанные процедуры мы реализуем так же по шагам, как и в алгоритме ТHAID. В итоге выделяются группы респондентов, каждая из которых описывается последовательностью значений рассматриваемых признаков (так, последовательность, отвечающая крайней правой “цепочке” с рисунка 19, состоит из двух элементов: среднее, неполное высшее или высшее образование; из служащих или военных). Наш алгоритм дает основание полагать, что каждой из таких выделенных последовательностей будет отвечать свое “поведение” соответствующей группы респондентов, т.е. свое, характерное именно для данной группы, распределение признака Y.
Заметим, что алгоритм CHAID, так же, как и THAID, не гарантирует выявления в исходных данных всех интересующих исследователя закономерностей. Основная причина – в том, что на каждом шаге разбиения алгоритм оценивает лишь двумерную связь. Он может заставить исследователя исключить из дальнейшего рассмотрения такой признак-предиктор, который, будучи сам по себе не очень “хорошим”, в сочетании с другими может дать наилучший результат. Скажем, некий предиктор, не имея связи с целевым и, в силу этого, отбрасываемый (из-за того, что условные распределения целевого признака, вычисленные для отдельных градаций предиктора, схожи друг с другом и поэтому не дают нам отдельные типы респондентов), в сочетании с каким-то другим предиктором может иметь сильную связь с целевым (в п. 2.3.6 мы приводили пример, когда связь между двумя не связанными признаками появляется при фиксации значения третьего признака). И эта связь может быть более значимой, чем связь между целевым признаком и отобранными алгоритмом предикторами.
Алгоритм задействован в известном пакете программ SPSS. Буквы “СН” в названии алгоритма – от греческой буквы “C” (Хи), поскольку критерий “Хи-квадрат” лежит в основе метода.
Отметим, что описанные алгоритмы охватывают не все те задачи поиска взаимодействий, которые интересуют социолога. Имеются другие направления анализа данных, включающие в себя несколько иные алгоритмы интересующего нас плана - алгоритмы поиска логических закономерностей, разработанные советскими авторами. Об этих алгоритмах пойдет речь в п.п. 2.5.5 и 2.5.6.
 2015-01-30
2015-01-30 1152
1152
