2015-01-30
450
Координатная форма записи этого варианта итерационного метода имеет вид:
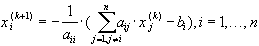. (27)
Формулы (27) получаются непосредственно из исходной системы, если i - ое уравнение системы разрешить относительно неизвестного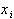 
.
Подставляя сюда
,
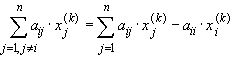получаем
или, в каноническом виде,
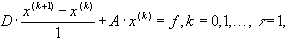
где 
- диагональная матрица.
В соответствии с теоремой 2 сходимость этого метода гарантирована, если положительны матрица A и матрица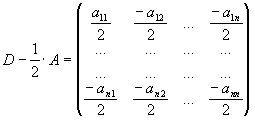 
Из положительности матрицы A вытекает, что ее диагональные элементы, а значит и диагональные элементы матрицы
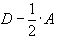больше нуля. При этом условии для положительности матрицы достаточно, чтобы она имела свойства диагонального преобладания 
.
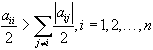Последнее равносильно тому, чтобы этим свойством обладала сама матрица A. Свойство диагонального преобладания матрицы A как достаточное условие сходимости метода Якоби возникает и в качестве следствия из теоремы 1.
