В качестве первого примера рассмотрим явный стационарный итерационный метод, каноническая форма которого:
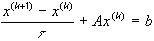 (26)
(26)
Выясним достаточные условия сходимости этого метода. В соответствии с теоремой 2 для этого достаточно, чтобы матрица системы A была симметричной и положительной и выполнялось неравенство 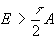
Учитывая, что 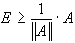 , имеем
, имеем 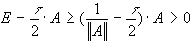 .
.
Это неравенство выполнено при 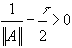 . Следовательно, метод простых итераций сходится при всех значениях
. Следовательно, метод простых итераций сходится при всех значениях 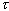 , удовлетворяющих неравенству
, удовлетворяющих неравенству 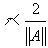 .
.
С учетом неравенства 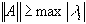 , где
, где 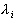 - собственные числа матрицы A, достаточное условие сходимости можно записать в виде
- собственные числа матрицы A, достаточное условие сходимости можно записать в виде

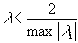
Условие (26) является также и необходимым для сходимости метода простых итераций.
Пусть 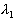 - максимальное по модулю собственное число,
- максимальное по модулю собственное число, 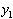 - соответствующий собственный вектор. При начальном приближении
- соответствующий собственный вектор. При начальном приближении 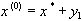 для погрешности k -го приближения имеем:
для погрешности k -го приближения имеем:
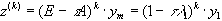 .
.
Тогда
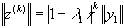 .
.
Если 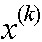 , то
, то 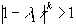 и
и 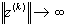 при
при 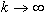 .
.
Если 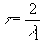 , то
, то 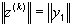 не стремится к нулю при
не стремится к нулю при 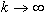 .
.
 2015-01-30
2015-01-30 395
395








