Остаточный член

В узлах 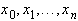многочлен Лагранжа совпадает с заданной функцией, в остальных точках в общем случае 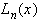не совпадает с 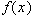(кроме случая, когда 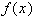многочлен степени не выше 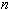). Разность 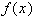- - 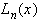остаточный член. Запишем ее в виде .

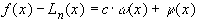При 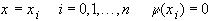. Найдем постоянную такую, чтобы 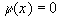в некоторой фиксированной точке 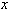, в которой мы рассматриваем погрешность.

Относительно 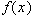будем предполагать 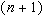кратную дифференцируемость.

Значение c, при котором 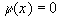существует и равно 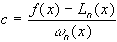. Тогда функция 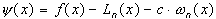равна нулю по крайней мере в 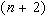точках .

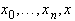По теореме Ролля производная 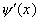равна нулю по крайней мере в 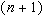точках 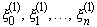. Далее, 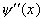равна нулю по крайней мере в n точках и т.д.

Для 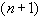- производной получаем, что существует по крайней мере одна точка 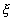такая, что .

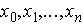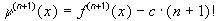
Отсюда получаем при 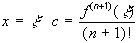. В этом случае в точке 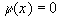, т.е. остаточный член в точке 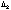имеет вид:

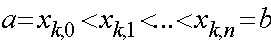
Значение 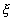зависит от 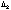- точки, в которой рассматривается погрешность.

Оценка остаточного члена:

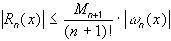, 3.2. Минимизация остаточного члена