Минимизация оценки остаточного члена

Пусть 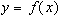приближена на отрезке 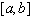интерполяционным многочленом степени 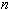. Оценка остаточного члена:

.

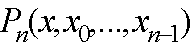Величина 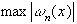на отрезке [-1,1] будет минимальна, если 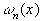окажется многочленом 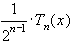. 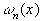совпадает с этим многочленом, если в качестве узлов интерполяции взять корни многочлена Чебышева 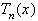, вычисляемые по формуле (12).

Сделаем замену 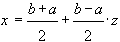, задающую отображение [-1, 1] в отрезок 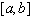. Отсюда . Тогда 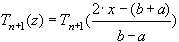и многочлен 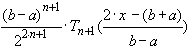является наименее уклоняющимся от нуля многочленом степени 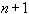со старшим коэффициентом 1 на отрезке 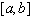. Нули определяются формулой

.

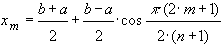
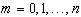Если в качестве узлов интерполяции взять эти значения, то

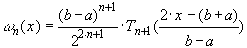и для нее на отрезке

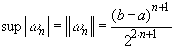- минимальная величина. Тогда оценка остаточного члена будет .

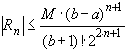[О комплексе|Теория|Практикум|Справочник по MathCAD'у|Об авторах]

[Home|Кафедра|ПетрГУ]

где 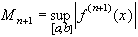3.3. Интерполяционная формула Ньютона с разделенными разностями

Пусть имеется табулированная функция . Введем понятие разделенной разности.