2015-01-30
284
, 
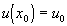
по начальным данным. Пусть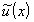 
- решение задачи Коши с начальным условием 
.
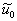Тогда для функции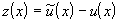 
можно написать дифференциальное уравнение
, 
, 
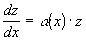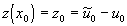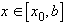
где
, 
.
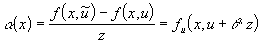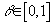Решая дифференциальное уравнение, получаем
,
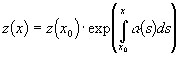следовательно, если наложить условие
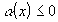, (т.е. 
),
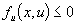то можно сделать вывод
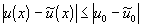
т.е. решение задачи устойчиво по начальным данным (погрешность не возрастает). Если же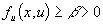 
, то получаем неравенство
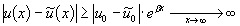
т.е. решение исходной задачи неустойчиво по начальным данным.
Решение задачи (2) ведет себя аналогично решению линейного дифференциального уравнения
, , , 
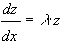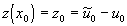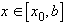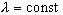, (3)
которое можно рассматривать как модельное при исследовании устойчивости. Решение этого уравнения имеет вид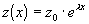 
, его модуль не возрастает при 
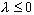, т.е.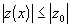 
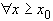, и решение устойчиво.
