Для составления квадратурной формулы применим интерполяционную формулу Ньютона с разделенными разностями (см. раздел 3.3). Введем функцию 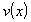 , определенную следующим образом:
, определенную следующим образом:
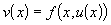 .
.
Тогда, как показано в разделе 3.3, можно интерполировать функцию 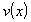 на отрезке
на отрезке 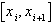 многочленом
многочленом
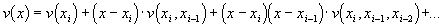
где 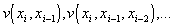 - разделенные разности. Выполним замену переменной по формуле
- разделенные разности. Выполним замену переменной по формуле 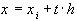 и введем обозначения
и введем обозначения
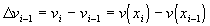 ,
,
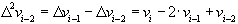 ,
,
............................................
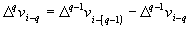
Учитывая, что
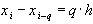 и
и 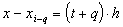 ,
,
можно выписать соотношения для разделенных разностей
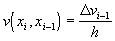 ,
, 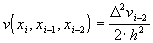 , и т.д.
, и т.д.
и записать интерполяционный многочлен в виде
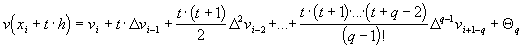 ,
,
где
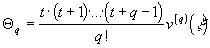 - остаточный член.
- остаточный член.
Тогда квадратурная формула для интеграла примет вид:
, (14)
где
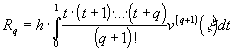 ,
,
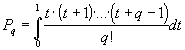 , в частности,
, в частности, 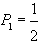 ,
, 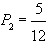 , и т.д.
, и т.д.
Таким образом, из формул (13) и (14) можно получить общий вид явной 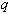 -шаговой схемы Адамса:
-шаговой схемы Адамса:
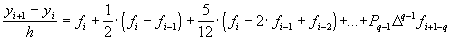
В частности, двухшаговая схема Адамса принимает форму
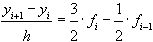 (15)
(15)
а трехшаговая схема имеет вид
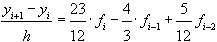 , где
, где 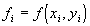 .
.
 2015-01-30
2015-01-30 378
378








