Исследуем устойчивость разностной схемы (15) на модельной задаче
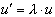 ,
, 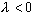 ,
, 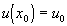 .
.
Для модельного уравнения схема примет вид
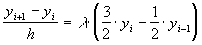
или
Ошибка! Закладка не определена..
Последнее уравнение является частным случаем трехточечного однородного разностного уравнения с постоянными коэффициентами:
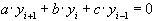 (16)
(16)
В уравнении (16) любое его решение однозначно определяется заданием значений в двух соседних узлах сетки. Действительно, зная 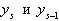 , находим
, находим 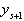 , и т.д. Если
, и т.д. Если 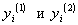 - два линейно независимых решения уравнения (16), то общее решение этого уравнения можно записать в виде линейной комбинации:
- два линейно независимых решения уравнения (16), то общее решение этого уравнения можно записать в виде линейной комбинации:
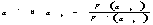 (17)
(17)
Убедимся, что формула (17) в самом деле дает общее решение уравнения (16). Пусть 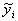 - некоторое решение (16), и
- некоторое решение (16), и 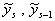 - его значения в узлах
- его значения в узлах 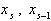 . Тогда из (17) получаем систему
. Тогда из (17) получаем систему
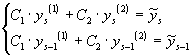
которая однозначно разрешима относительно 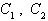 в силу линейной независимости решений
в силу линейной независимости решений 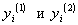 .
.
Общее решение (17) можно найти явно. Для этого находим два решения вида 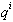 , подставляя
, подставляя 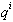 в уравнение (16). В таком случае получается квадратное уравнение относительно
в уравнение (16). В таком случае получается квадратное уравнение относительно 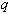 :
:
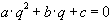 .
.
Для устойчивости разностной схемы должно выполняться неравенство
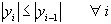 (18)
(18)
В нашем случае 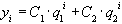 , поэтому неравенство (18) будет выполняться, если
, поэтому неравенство (18) будет выполняться, если 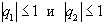 Квадратное уравнение для
Квадратное уравнение для 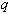 в нашем случае имеет вид
в нашем случае имеет вид
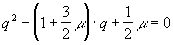 , где
, где 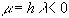 .
.
Заметим, что дискриминант этого уравнения всегда положителен, поскольку
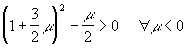 .
.
Кроме того, заметим, что в квадратном уравнении вида
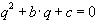
условие на корни 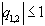 выполняется, если
выполняется, если 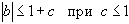 , т.к.
, т.к.
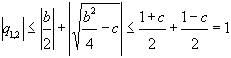 .
.
В нашем случае 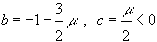 , поэтому условие устойчивости запишется как неравенство
, поэтому условие устойчивости запишется как неравенство
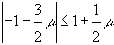 ,
,
выполняющееся при
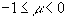 .
.
Таким образом, условие устойчивости двухточечной схемы Адамса на модельной задаче принимает вид 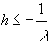 (допустимый шаг в два раза меньше, чем в схеме Эйлера).
(допустимый шаг в два раза меньше, чем в схеме Эйлера).
[О комплексе|Теория|Практикум|Справочник по MathCAD'у|Об авторах]
[Home|Кафедра|ПетрГУ]
 , (13)
, (13)
где
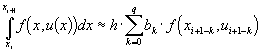
- квадратурная формула для интеграла. Очевидно, что формула (13) - частный случай разностной схемы (12).
[О комплексе|Теория|Практикум|Справочник по MathCAD'у|Об авторах]
[Home|Кафедра|ПетрГУ] 4.9. Неявные схемы Адамса
 2015-01-30
2015-01-30 338
338








