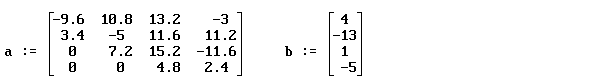
Записывается расширенная матрица
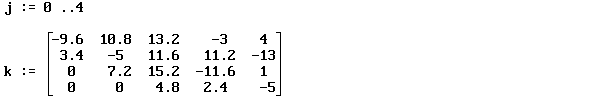
В матрице a выбирается максимальный по модулю элемент, который называется главным. На этот элемент делится строка расширенной матрицы, содержащая главный элемент.

Полученный результат записывается в матрицу k.
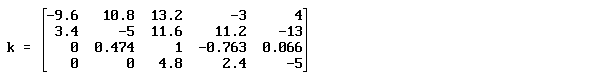
Из каждой строки матрицы k вычитается строка, содержащая главный элемент, умноженная на элемент, стоящий на пересечении текущей строки и столбца, содержащего главный элемент.
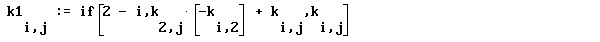
В результате коэффициенты при 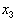 обращаются в нуль.
обращаются в нуль.
Дальнейшие вычисления производятся аналогично.



В результате получается расширенная матрица, состоящая из единичной матрицы и вектора-столбца.
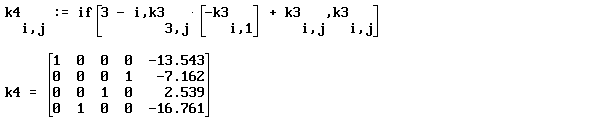
Вектор-столбец является решением исходной системы.

Решение системы линейных уравнений можно найти, используя операторы пакета для работы с матрицами.

1.3. Итерационные методы решения систем уравнений
1.3.1. Решение систем линейных алгебраических уравнений методом Зейделя.
Тема: Решение системы линейных уравнений методом Зейделя с точностью 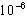 .
.
 2015-01-30
2015-01-30 582
582








