Метод половинного деления (дихотомии)

Сформулируем без доказательства очень важную для рассмотрения дальнейших вопросов теорему.

Теорема: Если непрерывная функция f (x) принимает значения разных знаков на концах отрезка [α, β], то есть f (α) ·f (β) < 0, то внутри этого отрезка содержится по меньшей мере один корень уравнения f (x) = 0, а именно: найдётся хотя бы одно число 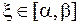такое, что f (ξ) = 0.

Пусть дано уравнение

f (x) = 0, (11.3)

где функция f (x) определена и непрерывна на интервале [ a, b ] и f (a) ·f (b) < 0. Для нахождения корня уравнения делим отрезок [ a, b ] пополам:

· если f ((a + b)/2) = 0, то ξ = (a + b)/2 является корнем уравнения (4.3);

· если 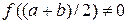, то выбираем ту половину отрезка [ a, (a + b)/2] или [(a + b)/2, b ], на концах которого функция f (x) имеет противоположные знаки. Новый суженный отрезок [ a₁, b₁ ] снова делим пополам и проводим тот же анализ и т.д.

Очевидно, что закончить уточнение значения корня можно при достижении условия |а_j– b_j| < ε, где ε > 0 - сколь угодно малое число. Второй способ закончить вычисления - задать максимальное значение невязки:
f ((a_j + b_j) /2) < ε.