Прямоугольная пластина (рис. К4.0–К4.4) или круглая пластина радиуса R =60 см (рис. К4.5–К4.9) вращается вокруг неподвижной оси по закону φ=f1(t) заданному в табл. К4. Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. На рис. 0, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3, 4, 7, 8, 9 ось вращения OO1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (рис. 0–4) или по окружности радиуса R (рис. 5–9)движется точка М; закон ее относительного движения, т. е. зависимость 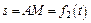 (s выражено в сантиметрах, t – в секундах), задан в таблице отдельно для рис. 0–4 и для рис. 5–9; там же даны размеры b и l. На рисунках точка - Д1 показана в положении, при котором
(s выражено в сантиметрах, t – в секундах), задан в таблице отдельно для рис. 0–4 и для рис. 5–9; там же даны размеры b и l. На рисунках точка - Д1 показана в положении, при котором 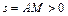 (при s <0 точка M находится по другую сторону от точки А).
(при s <0 точка M находится по другую сторону от точки А).
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t =l с.
Указания. Задача К1 – на сложное движение точки. Для ее решения воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка Л1 на пластине в момент времени t1= l c, и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунках к задаче).
В случаях, относящихся к рис. 5–9, при решении задачи не подставлять числового значения R, пока не будут определены положение точки М в момент времени t1= 1 с и угол между радиусами СМ и СА в этот момент.
Таблица К4
| Номер условия | Для всех рисунков φ=f1(t) | Для рис. 0–4 | Для рис. 5-9 | ||
| b, см | 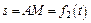 | l | 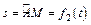 | ||
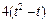 | 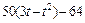 | R | 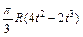 | ||
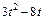 | 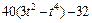 | 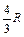 | 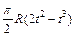 | ||
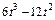 | 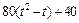 | R | 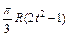 | ||
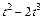 | 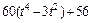 | R | 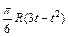 | ||
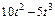 | 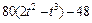 | R | 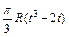 | ||
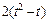 | 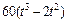 | R | 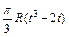 | ||
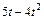 | 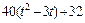 | 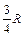 | 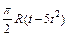 | ||
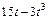 | 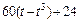 | R | 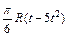 | ||
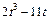 |  | R | 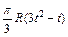 | ||
 |  |  |  |
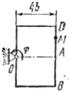 Рис. К4.0 Рис. К4.0 | 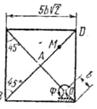 Рис. К4.1 Рис. К4.1 | 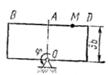 Рис. К4.2 Рис. К4.2 |
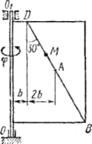 Рис. К4.3 Рис. К4.3 | 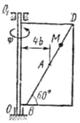 Рис. К1.4 Рис. К1.4 | 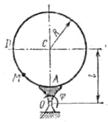 Рис. К4.5 Рис. К4.5 |
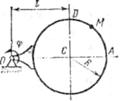 Рис. К4.6 Рис. К4.6 | 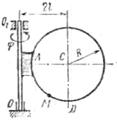 Рис. К4.7 Рис. К4.7 |
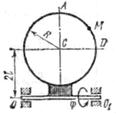 Рис. К4.8 Рис. К4.8 | 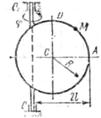 Рис. К4.9 Рис. К4.9 |
Пример К4. Шар радиуса R (рис. К4,а) вращается вокруг своего диаметра АВ по закону φ=f1(t) (положительное направление отсчета угла φ показано на рис. К4, а дуговой стрелкой). По дуге
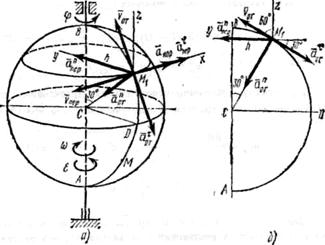
Рис. К4
большого круга («меридиану») 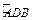 движется точка Л1 по закону
движется точка Л1 по закону 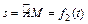 ; положительное направление отсчета s от А к D.
; положительное направление отсчета s от А к D.
Дано: R =0,5 м, 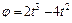 ,
, 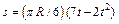 (φ – в радианах, s – в метрах, t – в секундах). Определить: vab и аaб в момент времени t1 =l с.
(φ – в радианах, s – в метрах, t – в секундах). Определить: vab и аaб в момент времени t1 =l с.
Решение. Рассмотрим движение точки М как сложное, считая ее движение по дуге ADB относительным (АВ– относительная траектория точки), а вращение шара – переносным движением. Тогда абсолютная скорость 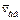 и абсолютное ускорение
и абсолютное ускорение 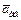 точки найдутся по формулам:
точки найдутся по формулам:
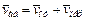 ,
, 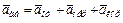 , (1)
, (1)
где, в свою очередь, 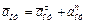 ,
, 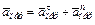 .
.
Определим все характеристики относительного и переносного движений.
1. Относительное движение. Это движение происходит по закону
 (2)
(2)
Сначала установим, где будет находиться точка M на дуге 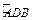 в момент времени t1. Полагая в уравнении (2) t =1 с, получим
в момент времени t1. Полагая в уравнении (2) t =1 с, получим
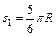 . Тогда
. Тогда 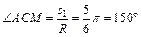
или 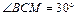 . Изображаем на рис. К4, а точку в положении, определяемом этим углом (точка M1).
. Изображаем на рис. К4, а точку в положении, определяемом этим углом (точка M1).
Теперь находим числовые значения 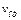 ,
, 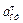 ,
, 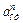 :
:
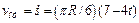 ;
; 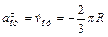 ;
;
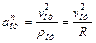
где ρот – радиус кривизны относительной траектории, т. е. дуги 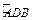 .Для момента времени t1= 1 c, учитывая, что R =0,5 и, получим
.Для момента времени t1= 1 c, учитывая, что R =0,5 и, получим
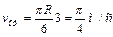 ;
; 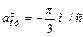 ; (3)
; (3)
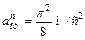 .
.
Знаки показывают, что вектор  направлен в сторону положительного отсчета расстояния s, а вектор
направлен в сторону положительного отсчета расстояния s, а вектор 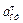 – в противоположную сторону; вектор
– в противоположную сторону; вектор 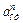 - направлен к центру С дуги
- направлен к центру С дуги 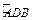 . Изображаем все эти векторы на рис. К4, а. Для наглядности приведен рис. К4, б, где дуга
. Изображаем все эти векторы на рис. К4, а. Для наглядности приведен рис. К4, б, где дуга 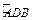 совмещена с плоскостью чертежа.
совмещена с плоскостью чертежа.
2. Переносное движение. Это движение (вращение) происходит по закону 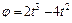 . Найдем угловую скорость ω и угловое ускорение ε переносного вращения:
. Найдем угловую скорость ω и угловое ускорение ε переносного вращения: 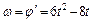 ,
, 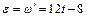 и при t1 =l с.
и при t1 =l с.
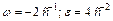 . (4)
. (4)
Знаки указывают, что при t1 =l с направление ε совпадает с направлением положительного отсчета угла φ, а направление ω ему противоположно; отметим это на рис. К4, а соответствующими дуговыми стрелками.
Для определения 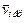 и
и 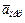 находим сначала расстояние h точки А1, от оси вращения. Получаем
находим сначала расстояние h точки А1, от оси вращения. Получаем 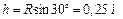 . Тогда в момент времени t1 =1 с, учитывая равенства (4), получим:
. Тогда в момент времени t1 =1 с, учитывая равенства (4), получим:
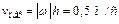 ,
, 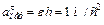 , (5)
, (5)
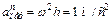 .
.
Изображаем на рис. К4, а векторы 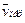 и
и 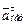 с учетом направлений ω и ε и вектор
с учетом направлений ω и ε и вектор 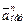 (направлен к оси вращения).
(направлен к оси вращения).
3. Кориолисово ускорение. Так как угол между вектором 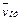 и осью вращения (вектором
и осью вращения (вектором 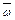 ) равен 60°, то численно в момент времени t1 =1 с (см. равенства (3) и (4))
) равен 60°, то численно в момент времени t1 =1 с (см. равенства (3) и (4))
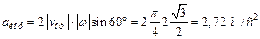 (6)
(6)
Направление 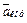 найдем, спроектировав вектор
найдем, спроектировав вектор 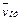 на плоскость, перпендикулярную оси вращения (проекция направлена так же, как вектор
на плоскость, перпендикулярную оси вращения (проекция направлена так же, как вектор 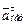 ), и повернув затем эту проекцию в сторону ω,т. е. по ходу часовой стрелки, на 90°. Иначе направление
), и повернув затем эту проекцию в сторону ω,т. е. по ходу часовой стрелки, на 90°. Иначе направление 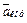 можно найти, учтя, что
можно найти, учтя, что 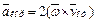 . Изображаем вектор
. Изображаем вектор 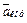 на рис. К4, а.
на рис. К4, а.
Теперь можно вычислить значения vаб и aаб.
4. Определение vаб. Так как 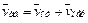 ,а векторы
,а векторы 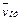 и
и 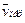 взаимно перпендикулярны (см. рис. К4, а),то в момент времени t1 =1 с.
взаимно перпендикулярны (см. рис. К4, а),то в момент времени t1 =1 с.
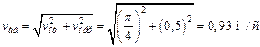
5. Определение aаб. По теореме о сложении ускорений
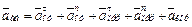 (7)
(7)
Для определения aаб проведем координатные оси 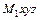 (см. рис. К4, а)и вычислим проекции вектора
(см. рис. К4, а)и вычислим проекции вектора 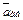 на эти оси. Учтем при этом, что векторы
на эти оси. Учтем при этом, что векторы 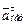 и
и 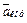 лежат на проведенной оси x,а векторы
лежат на проведенной оси x,а векторы 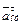 ,
, 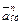 и
и 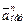 расположены в плоскости дуги
расположены в плоскости дуги 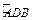 , т. е. в плоскости
, т. е. в плоскости 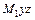 (см. рис. К4,б). Тогда, проектируя обе части равенства (7) на координатные оси и учтя одновременно равенства (3), (5), (6), получим для момента времени t1 =1.
(см. рис. К4,б). Тогда, проектируя обе части равенства (7) на координатные оси и учтя одновременно равенства (3), (5), (6), получим для момента времени t1 =1.
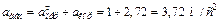 ;
;
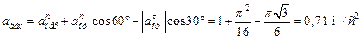 ;
;
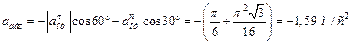 .
.
Отсюда находим значение aаб в момент времени t1= 1с:
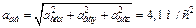
Ответ: vаб =0,93 м/с; ааб =4,1 м/с2.
 2015-01-30
2015-01-30 1613
1613








