4.1. Постановка прямой и обратной задачи расчёта показателей надёжности
Задача расчёта показателей надёжности формулируется следующим образом. Имеется объект, состоящий из нескольких частей. Известны показатели надёжности каждой составной части. Требуется рассчитать общий показатель надёжности объекта в целом. Пример 4.1: имеется объект из трёх частей. Наработки на отказ каждой части равны соответственно 10 часов, 25 часов и 40 часов. В результате расчёта найден общий показатель надёжности объекта в целом (наработка на отказ), равный 6,1 часа. Эта задача иногда именуется прямой задачей расчёта надёжности.
Кроме прямой существует обратная задача: распределить общий показатель надёжности объекта в целом между его составными частями так, чтобы в результате прямого расчёта надёжности по полученным исходным данным (показателям надёжности каждой составной части) вновь рассчитанный общий показатель надёжности объекта в целом равнялся исходному показателю, подлежащему распределению между составными частями объекта. Задача решается при наличии ряда ограничений-условий. Пример 4.2: имеется объект из трёх частей. Общий показатель надёжности объекта в целом (наработка на отказ) равна 6,1 часа. Требуется распределить общий показатель надёжности объекта в целом 6,1 часа между его составными частями. Вариант 1 решения – ограничений-условий нет. В этом случае существует множество решений, одним из которых является и решение «Наработки на отказ каждой части равны соответственно 10 часов, 25 часов и 40 часов». Вариант 2 решения – ограничение-условие сформулировано в виде: каждая из составных частей имеет свою сложность, определяемую, например, числом входящих в неё более мелких примерно равносложных компонентов. Распределение показателей надёжности должно учитывать эту сложность по принципу: чем выше сложность, тем ниже должна быть распределяемая наработка на отказ. Пример 4.3. Первая составная часть включает примерно 100 равносложных компонентов, вторая – примерно 200, третья – примерно 500. Требуется распределить общий показатель надёжности объекта в целом 6,1 часа между его составными частями при наличии вышеприведенного ограничения-условия. Решение – в подразделе 4.3. Вариант 3 решения – ограничение-условие сформулировано в виде: первая составная часть (мозг) должна быть в 10 раз надёжнее (по интенсивности отказов) третьей составной части (руки и ноги) и в 2 раза надёжней второй составной части (сердце). Решение – в подразделе 4.4.
Проще всего рассчитывать показатели надёжности КТС (комплекса технических средств), поскольку, как следует из лекции 1, надёжность КТС оценивается с 1940-х годов, а надёжность ПО (программного обеспечения) – только с 1980-х, следовательно методики расчёта надёжности КТС более разработаны, чем для ПО. Кроме того, для простоты расчёта целесообразно предположить экспоненциальный закон распределения отказов.
4.2. Расчёт надёжности КТС при последовательном соединении элементов в надёжностном смысле
Последовательном соединении элементов в надёжностном смысле означает, что отказ любого из элементов приводит к отказу КТС в целом. Это означает, что вероятность безотказной работы 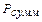 системы с интенсивностью отказов
системы с интенсивностью отказов 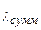 , состоящей из N элементов, каждый i -й из которых обладает интенсивностью отказов
, состоящей из N элементов, каждый i -й из которых обладает интенсивностью отказов 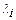 , равна произведению таких же вероятностей
, равна произведению таких же вероятностей 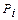 элементов, т.е.
элементов, т.е.
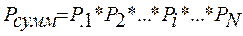 (4.1)
(4.1)
Подставляя в формулу (4.1) формулы для вероятности безотказной работы при экспоненциальной модели отказа (табл. 3.1)
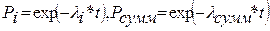 , (4.2)
, (4.2)
получим
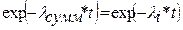 . (4.3)
. (4.3)
Выражение (4.3) легко преобразуется к виду
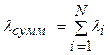 (4.4)
(4.4)
Для учёта влияния условий эксплуатации формулу (4.4) дополняют к виду
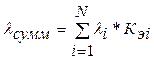 (4.5)
(4.5)
При этом в (4.5) 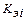 – коэффициент эксплуатации, зависящий от параметров эксплуатации элемента. Таблицы зависимости названных коэффициентов от параметров эксплуатации, а также значения
– коэффициент эксплуатации, зависящий от параметров эксплуатации элемента. Таблицы зависимости названных коэффициентов от параметров эксплуатации, а также значения 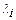 для различных элементов КТС приведены в [48]. Например, для керамических конденсаторов часть необходимой таблицы [48, с. 21] имеет вид
для различных элементов КТС приведены в [48]. Например, для керамических конденсаторов часть необходимой таблицы [48, с. 21] имеет вид
Таблица 4.1
Зависимость 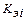 от температуры и электрической нагрузки
от температуры и электрической нагрузки
| Температура, градусов Цельсия | 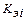 при U/Uном при U/Uном | |||
| 0,1 | 0,2 | 0,3 | 0,4 | |
| 0,14 | 0,17 | 0,22 | 0,28 | |
| 0,15 | 0,18 | 0,24 | 0,30 | |
| 0,16 | 0,20 | 0,26 | 0,32 |
Меньшая по объёму, чем в [48], таблица значений 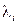 приведена в [49, с. 59-61]. Там же на с. 62 даны коэффициенты эксплуатации (также в объёме, меньшем, чем в [48]), учитывающие не только электрическую нагрузку и влияние температуры (эффект Аррениуса), но и поправку на место установки аппаратуры (лаборатория или офис, полевые условия, борт самолёта или морского судна). При расчёте следует учесть и надёжность паяных соединений (паек), а также обжимных соединений, которые для аппаратуры, прошедшей термоциклирование при изготовлении, можно принять [49, с. 59] равными для паек lI =10-8 1/час, а для обжимных соединений lI =2 10-8 1/час.
приведена в [49, с. 59-61]. Там же на с. 62 даны коэффициенты эксплуатации (также в объёме, меньшем, чем в [48]), учитывающие не только электрическую нагрузку и влияние температуры (эффект Аррениуса), но и поправку на место установки аппаратуры (лаборатория или офис, полевые условия, борт самолёта или морского судна). При расчёте следует учесть и надёжность паяных соединений (паек), а также обжимных соединений, которые для аппаратуры, прошедшей термоциклирование при изготовлении, можно принять [49, с. 59] равными для паек lI =10-8 1/час, а для обжимных соединений lI =2 10-8 1/час.
Пример 4.4 расчёта надёжности КТС. Исходные данные для расчёта надёжности вычислительного устройства, полученные на основе анализа КД, имеют вид:
Таблица 4.2
Исходные данные для расчёта надёжности вычислительного устройства
| Наименование элемента | Количество в КТС | 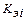 | Примечание |
| 1. ИС 16-выводныя микропроцессорная серии К535 | |||
| 2. Стабилитрон КС 113А кремниевый | Т=35 градусов С Ток/ток макс=0,7 | ||
| 3. Конденсатор алюминиевый электролитический К50-25 | Т=40 градусов С Напряжение/ напряжение макс=0,9 | ||
| 4. Трансформатор силовой ТС-40 | Т=50 градусов С Мощность/мощность ном=0,6 | ||
| 5. Переключатель кнопочный ПК-11 | |||
| 6. Разъём РППМ22 22-выводной |
Для расчёта рекомендуется использовать формулу (4.5) и справочник [48]. Количество паек следует подсчитать суммированием паяных соединений по каждому из элементов табл. 4.2, не забывая об их количестве. В итоге расчёта имеем 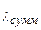 = 1/ч, а наработка на отказ КТС
= 1/ч, а наработка на отказ КТС 
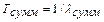 = 1/……. == ……(ч).
= 1/……. == ……(ч).
Полученные в итоге расчёта надёжности результаты анализируются разработчиком совместно с заказчиком. При превышении заданных требований к надёжности полученных в результате расчёта величин заказчик и разработчик имеют 2 варианта дальнейшего проведения работ. 1-й вариант – согласиться на снижение требований к надёжности. 2-й вариант – при наличии средств и времени на основании такого анализа может быть принято решение о переработке схемы электрической принципиальной КТС в части а) выбора более надёжного КТС б) облегчения нагрузок (условий эксплуатации), в которых работают отдельные элементы
Пример 4.5 расчёта надёжности КТС. Исходные данные для расчёта надёжности ВС, полученные на основе анализа КД и данных из работы [50] имеют вид:
Таблица 4.3
Исходные данные для расчёта надёжности ВС
| Наименование элемента | Коли- чество | Наработка на отказ,тыс. ч | Интенси- вность отказов, (1/ч)*10-6 | Общая интенсив-ность отказов по строке, (1/ч)*10-6 | Примечание |
| 1. Компьютер фирмы (ф.) Ostagon Systems | 17,5 | 57,1 | |||
| 2. Источник вторичного эле-ктропитания PW -250 ф. Portwell | |||||
| 3. Контроллер 5815 жёстких дисков ф. Ostagon Systems | 71,5 | ||||
| 4. НЖД типа WDE18300/AV ф. Western Digital | |||||
| 5. Доп. компонен-ты компьютера ф. Ostagon Systems, в т.ч. сетевой адаптер 5500 | 2,97 | ||||
| 6. Видеоадаптер 2430 | 2,94 | ||||
| 7. Плата последо-вательного интерфейса 5554 | 1,33 | ||||
| 8. Многофункцио-нальная плата вв/ выв с паралле-льным портом и портом клавиатуры | 1,34 | ||||
| 9. Монитор | 27,2 | 36,8 | |||
| 10, 11. Мышь и клавиатура | ≈0 | Немедленно заменяются на работоспособные при отказе | |||
| Итого | 430 1/ч = 2330 ч |
4.3. Расчёт надёжности КТС при параллельном соединении элементов в надёжностном смысле
4.3.1. Общие положения. Аналогичным образом можно рассчитать и надёжность КТС при параллельном соединении элементов КТС. Параллельное соединение означает, что отказ любого из элементов не приводит к отказу КТС в целом. Отказ КТС в целом наступает при отказе всех элементов. Это легко проиллюстрировать примером двухканальной системы обработки информации. Каждый канал – элемент системы. При отказе одного из каналов система не теряет работоспособность по второму каналу, который продолжает обрабатывать информацию. В этом случае суммарная вероятность отказа 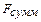 для системы из двух элементов, каждый из которых имеет вероятность отказа
для системы из двух элементов, каждый из которых имеет вероятность отказа 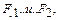 равна
равна
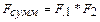 (4.6)
(4.6)
Подставляя в (4.1) значения 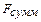 , а также
, а также 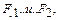 найденные из (3.2), получим
найденные из (3.2), получим
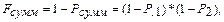 (4.7)
(4.7)
откуда
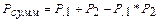 . (4.8)
. (4.8)
Несложно показать, например, на двух пересекающихся окружностях разного диаметра, что формула (4.1) реализует логическую операцию И ((логическое произведение или для множеств S1 и S2 их пересечение S3 = S1 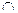 S2 /множество всех элементов, содержащихся и в S1, и в S2/), а формула (4.8) – логическую операцию ИЛИ (логическую сумму или объединение S3 = S1
S2 /множество всех элементов, содержащихся и в S1, и в S2/), а формула (4.8) – логическую операцию ИЛИ (логическую сумму или объединение S3 = S1 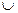 S2, S1+S2 множеств /множество всех элементов, содержащихся либо в S1, либо в S2, либо и в S1, и в S2/).
S2, S1+S2 множеств /множество всех элементов, содержащихся либо в S1, либо в S2, либо и в S1, и в S2/).
4.3.2. Анализ понятий «Последовательное и параллельное соединение элементов СКС в надёжностном смысле». Суть понятий «Последовательное соединение элементов СКС в надёжностном смысле» и «Параллельное соединение элементов СКС в надёжностном смысле» изложена в пункте 1. Сравнение методов расчёта надёжности при последовательном и параллельном соединении элементов показывает, что:
1) расчёт при последовательном соединении элементов проще и понятнее расчёта при параллельном соединении,
2) оценка показателя безотказности, полученная в предположении последовательного соединения элементов, будет ниже, чем аналогичная при параллельном соединении, поэтому первую оценку будем считать минимальной оценкой безотказности, а вторую – максимальной.
3) выбор того или другого типа соединения элементов в надёжностном смысле зависит от изложения критериев отказов в документации. Если записанным, например в паспорт СКС, критерием отказа СКС является выход из строя любого элемента СКС (при этом СКС будет продолжать работать, но с меньшей эффективностью), то следует использовать только «Последовательное соединение элементов СКС в надёжностном смысле». Если же запись критерия отказа в паспорт СКС не содержит требований по эффективности (например, работоспособной признаётся СКС только с 2-мя компьютерами или каналами), то следует использовать «Параллельное соединение элементов СКС в надёжностном смысле».
4.4. Решения обратной задачи расчёта показателей надёжности
В подразделе 4.1 остались нерешёнными 2 обратные задачи расчёта показателей надёжности. Их можно решить, используя материал подразделов 4.2-4.3. Итак,
Пример 4.3. Первая составная часть включает примерно 100 равносложных компонентов, вторая – примерно 200, третья – примерно 500. Требуется распределить общий показатель надёжности объекта в целом 6,1 часа между его составными частями при наличии вышеприведенного ограничения-условия. Решение. Всего равносложных компонентов
100+200+500 = 800 (компонентов).
Следовательно, на один равносложный компонент приходится интенсивность отказов
1/6,1 /800 = 0,000205 (1/час)
Это значит, что интенсивности отказов и наработки на отказ составных частей равны
Первой части – интенсивность 0,000205*100 = 0,0205 (1/час), наработка 1/0,0205 = 48,8 ч,
Второй части – интенсивность 0,000205*200 = 0,0410 (1/час), наработка 1/0,0410 = 24,4 ч,
Третьей части – интенсивность 0,000205*500 = 0,1025 (1/час), наработка 1/0,1025 = 9,76 ч,
Проверка – 0,0205+0,0410+0,1025=0,1640, 1/01640 = 6,1 ч.
Пример 4.8. Вариант 3 решения – ограничение-условие сформулировано в виде: первая составная часть (мозг) должна быть в 10 раз надёжнее (по интенсивности отказов) третьей составной части (руки и ноги) и в 2 раза надёжней второй составной части (сердце). Решение. Сумма индексов надёжности –
мозг/сердце/руки и ноги = 10/5/1 = 10+5+1 = 16.
Следовательно, на один индекс приходится интенсивность отказов
1/6,1 /16 = 0,01026 (1/час)
Тогда интенсивности отказов и наработки на отказ составных частей равны
Первой части – интенсивность 0,01026*10 = 0,1026 (1/час), наработка 1/0,1026 = 9,75 ч,
Второй части – интенсивность 0,01026*5 = 0,0513 (1/час), наработка 1/0,0513 = 19,5 ч,
Третьей части – интенсивность 0,01026= 0,01026 (1/час), наработка 1/0,01026 = 97,5 ч,
Проверка – 0,1026+0,0513+0,01026=0,1642, 1/01642 = 6,1 ч.
 2015-01-30
2015-01-30 1902
1902








