3.1. Понятие модели отказа
Исчерпывающей характеристикой любой случайной величины является её функция распределения. Нижеприведенные определения даны по ГОСТ [2]. Функция, или интегральная функция распределения случайной величины – это вероятность того, что значение случайной величины Х не превысит переменной величины х, т.е. Р(Х<=х).
Обозначим через t время работы до отказа (для невосстанавливаемого объекта), на отказ или между отказами (для восстанавливаемого объекта) или суммарную наработку объекта соответственно до отказа, на отказ или между отказами. Далее для простоты отвлечёмся от понятий «восстанавливаемый» и «невосстанавливаемый» объект, и названную переменную t упрощённо будем называть наработкой до отказа. Возникновение отказа – случайное событие, поэтому наработка τ от начального момента до возникновения этого события – случайная величина. Тогда вероятность F(t) того, что значение τ не превысит переменной величины t, т.е. F(τ<=t),
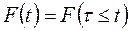 (3.1)
(3.1)
называется моделью отказов (или функцией распределения наработки до отказа, или интегральной функцией распределения наработки до отказа, или интегральным законом распределения (ИЗР) наработки до отказа, или вероятностью отказа). Противоположная вероятность
|
|
|
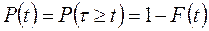 (3.2)
(3.2)
называется вероятностью безотказной работы (ВБР), а в ГОСТе [2] – моделью надёжности. В старой литературе (примерно 1959-1970 гг.) ВБР называли также функцией надёжности. ВБР является функцией наработки t. Обычно эту функцию предполагают непрерывной и дифференцируемой. Поэтому Р(t) связана с вероятностью отказа F(t) и плотностью распределения f(t) наработки до отказа (дифференциальным законом распределения (ДЗР) наработки до отказа) соотношением (3.3):
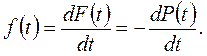 (3.3)
(3.3)
Из (3.3) следует, что обратная взаимосвязь (выражение ИЗР через ДЗР) имеет вид:
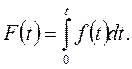 (3.4)
(3.4)
|
|
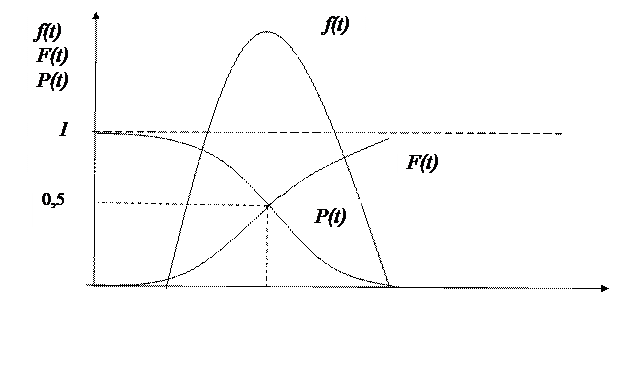
Рис. 3.1. Взаимосвязь плотности распределения наработки до отказа (ДЗР) и моделей отказа (ИЗР) и надёжности согласно (3.2), (3.3) для симметричного ДЗР.
При этом 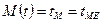
Широко применяется также понятие интенсивность отказов λ(t) – условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ ещё не возник.Интенсивность отказов λ(t) определяют по формуле:
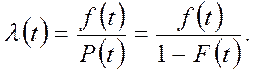 (3.5)
(3.5)
Следует отметить, что определение интенсивности отказов, приведенное выше, взято из ГОСТа [43]. В то же время в литературе «золотого века надежности» (период с 1958 по 1991 годы) часто встречается более понятное определение интенсивности отказов. В частности, в [4, с. 14] и в [21] интенсивностью отказов называется отношение числа отказавших образцов аппаратуры в единицу времени к среднему числу образцов, продолжающих исправно работать.
|
|
|
3.2. Основные характеристики модели отказа и их расчёт
ДЗР удобно характеризовать некоторыми временными характеристиками, именуемыми характеристиками положения или характерными точками распределения, а также вторым моментом (дисперсией), характеризующей разброс случайной наработки относительно важнейшей характеристики положения – математического ожидания M(t) (м.о.) наработки t до отказа. Для непрерывной случайной наработки t до отказа её м.о. (первый момент) равно
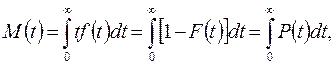 (3.6)
(3.6)
а дисперсия –
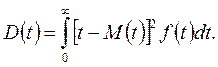 (3.7)
(3.7)
Среднеквадратичное отклонение σ (с.к.о.) есть корень из дисперсии, т.е.
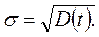 (3.9)
(3.9)
Модой tM непрерывной случайной наработки t является то её значение, в котором плотность распределения f(t) максимальна: 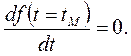 (3.10)
(3.10)
В общем случае асимметричного распределения м.о. его и его мода не совпадают. Медианой tMЕ непрерывной случайной наработки t называют такое её значение, для которого
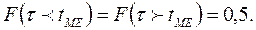 (3.11)
(3.11)
Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой f(t), делится пополам.
Расчёт статистических характеристик модели отказа прерывной случайной наработки или времени восстановления tk проводится для N их значений (k=1, 2,... N) по следующим формулам:
3.2.1. Математическое ожидание
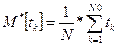 (3.12)
(3.12)
3.2.2. Дисперсия

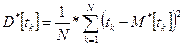 (3.13)
(3.13)
3.2.3. Среднеквадратичное отклонение 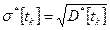 (3.14)
(3.14)
3.3. Основные модели отказов и их характеристики.
Основные модели отказов и их характеристики приведены в табл. 3.1.
3.4. Свойства основных моделей отказов
Следующие свойства моделей отказов следует запомнить:
3.4.1. Экспоненциальное распределение. Является частным случаем распределения Вейбулла и гамма-распределения. Поскольку реальная типичная кривая зависимости интенсивности отказов во времени имеет вид, показанный на рис. 3.2, то экспоненциальное распределение описывает только период нормальной эксплуатации и характеризуется на этом периоде постоянной интенсивностью отказов (см. (3.14)). Последнее показывает, что экспоненциальное распределение абсолютно не учитывает как ранние отказы, так и старение и износ, где его использовать нецелесообразно.

Рис. 3.2. Типичная кривая зависимости интенсивности отказов от времени
Для экспоненциального распределения при 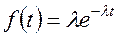 (3.15)
(3.15)
формула (3.2) легко выражается через (3.4)
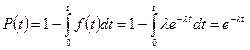 , (3.16)
, (3.16)
а формула (3.5) – через (3.15) и (3.16)
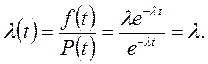 (3.17)
(3.17)
Резко упрощаются для экспоненциального распределения формулы (3.6) и (3.8)
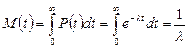 (3.18)
(3.18)
Таблица 3.1
Основные модели отказов по ГОСТ [2] (1-7) и монографии [4] (0,8-9)
| Наименование распределения | М.о. M(t) | Медиана tME | Мода tM | Дисперсия D(t) | С.к.о. 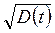 | |
| ДЗР f(t) | модель отказа ИЗР F(t) | |||||
| 0. Равномерное | 0,5 (а+ b) | 0,5 (а+b) | (а+b)2 /12 | (а+b) /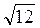 | ||
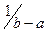 при b>t>а, 0 при t>b, а>t при b>t>а, 0 при t>b, а>t | 0 при а>t, 1 при t>b, 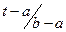 при b>t>а при b>t>а | |||||
| 1.Экспоненциальное | 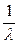 | 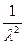 | 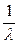 | |||
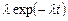 | 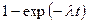 | |||||
| 2. Логарифмически нормальное | 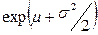 | 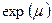 | 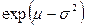 | 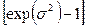 * * * * 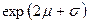 | ||
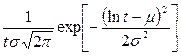 | 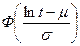 | |||||
| 3. Вейбулла | 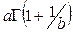 | 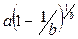 | 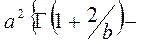 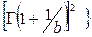 | |||
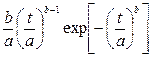 | 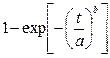 | |||||
| 4. Нормальное | m | m | m | σ2 | σ | |
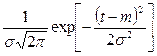 | 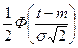 | |||||
| 5. Альфа– распределение (Г.В.Дружинина) | 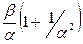 | 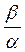 | 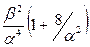 | |||
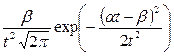 | 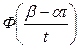 | |||||
| Наименование распределения | М.о. M(t) | Медиана tME | Мода tM | Дисперсия D(t) | С.к.о. 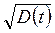 | |
| ДЗР f(t) | модель отказа ИЗР F(t) | |||||
| 6. DM – распределение (диффузионное монотонное) | 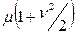 | μ | 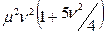 | |||
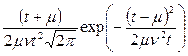 | 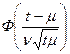 | |||||
8. Гамма-распределение 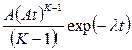 | 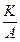 | 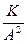 | 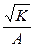 | |||
9. Релея 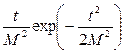 | 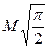 | 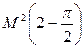 | ||||
| Дискретные распределения: 11. Пуассона | 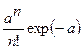 | A | a |
Примечания к табл. 2.1:
* 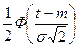 – табличный интеграл вероятностей или интеграл Лапласа, имеющий вид
– табличный интеграл вероятностей или интеграл Лапласа, имеющий вид 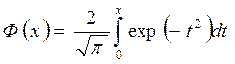
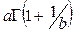 – гамма распределение, имеющее вид
– гамма распределение, имеющее вид
3.4.2. Р аспределение Вейбулла. Является используемым для кривой интенсивности отказов на периоде ранних отказов (при b<1 интенсивность отказов монотонно убывает) и на периоде ресурсных отказов (при b>1 интенсивность отказов монотонно возрастает). При b=1 распределениеВейбулла превращается в экспоненциальное.
3.4.3. Нормальное распределение. Параметры его m и σ являются математическим ожиданием и среднеквадратичным отклонением распределения, причём всё рассеивание случайной наработки относительно её м.о. m с точностью до долей процента укладывается в интервал [ m-3σ, m-3 ]. Мода и медиана нормального распределения совпадают с его м.о., причём максимальная ордината кривой плотности нормального распределения, соответствующая абсциссе, равной моде, медиане и м.о., составляет 1/2πσ.
|
|
|
3.5. Показатели надёжности – классификация, нормирование, состав
3.5.1. Классификация показателей. Показатель надежности – это количественная характеристика одного ила нескольких свойств, составляющих надежность объекта. Показатели надёжности делятся (по числу характеризуемых ими свойств, составляющих надежность объекта) на единичные и комплексные. Единичный показатель надежности – это показатель, характеризующий одно из свойств, составляющих надежность объекта, комплексный показатель – показатель, характеризующий несколько свойств, составляющих надежность объекта. Примеры: наработка на отказ, среднее время восстановления – единичные показатели, коэффициент готовности – комплексный показатель.
Показатели надёжности делятся также (по периоду жизненного цикла объекта, в котором собраны исходные данные для оценки показателя) на расчётные, экспериментальные и эксплуатационные. Расчётный показатель надежности – это показатель, значения которого определяются расчетным методом (чаще всего на этапе проектирования объекта). Экспериментальный показатель надежности – это показатель, точечная или интервальная оценка которого определяется по данным испытаний (чаще всего на этапе предварительных или приёмосдаточных испытаний). Эксплуатационный показатель надежности – это показатель, точечная или интервальная оценка которого определяется по данным эксплуатации (чаще всего на этапе эксплуатации).
3.5.2. Нормирование показателей и задание требований к ним. Установление в нормативно-технической документации и (или) конструкторской (проектной) документации количественных и качественных требований к надежности, называется нормированием надежности. Нормирование надежности включает выбор номенклатуры нормируемых показателей надежиости; технике-экономическое обоснование значений показателей надежности объекта и его составных частей; задание требований к точности и достоверности исходных данных; формулирование критериев отказов,.повреждений и предельных состояний; задание требований к методам контроля надежности на всех этапах жизненного цикла объекта. По наличию регламентации их в документации показатели надёжности делятся также нормируемые и ненормируемые. Нормируемый показатель надежности – это показатель, значение которого регламентировано нормативно-технической и (или) конструкторской (проектной) документацией на объект.
|
|
|
Задание требований к показателям надёжности также производится в нормативно-технической и (или) конструкторской (проектной) документации на объект, так как нормирование показателей надежности и задание требований к показателям надёжности – это одно и то же. Конструкторским документом, куда на стадии проектирования в составе других требований записываются требования к показателям надёжности (см. [15]), является техническое задание (ТЗ), а после проектирования: а) для серийного изделия – технические условия (ТУ), б) для остальных видов изделий – по согласованию между разработчиком и заказчиком один или несколько из следующих документов – стандарт, ТУ, паспорт, формуляр (ФО), техническое описание (ТО), инструкция по эксплуатации (ИЭ).
3.5.3. Состав единичных показателей надёжности восстанавливаемых объектов. Показатели безотказности:
а) ВБР согласно (3.2) – вероятность того, что в пределах заданной наработки отказ объекта не возникнет, б) средняя наработка на отказ согласно (3.6) как математическое ожидание наработки до отказа – отношение суммарной наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки, в) интенсивность отказов согласно (3.5) – условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента временя отказ не возник.
Показатели ремонтопригодности:
а) вероятность восстановления – вероятность того, что время восстановления работоспособного состояния объекта не превысит заданное значение, б) среднее время восстановления – математическое ожидание времени восстановления работоспособного состояния объекта после отказа.
Показатели сохраняемости и долговечности СВТ и ПО записывать не будем, так как вряд ли будем хранить ПО, а за время оценки долговечности СВТ и ПО морально устареет на все 100%.
3.6. Коэффициент готовности как основной комплексный показатель надёжности
Как показано выше, средняя наработка на отказ восстанавливаемого объекта Т и его среднее время восстановления ТВ – это характерные точки законов распределения случайных величин «наработка на отказ» и «время восстановления работоспособного состояния», конкретно их математические ожидания. Перечисленные показатели называются единичными показателями надёжности объекта, потому что первый из них характеризует только одно свойство надёжности (безотказность), а второй – тоже одно свойство (ремонтопригодность). Однако имеются показатели надёжности, которые характеризуют одновременно несколько свойств надёжности. Такие показатели называются комплексными. Самый известный комплексный показатель надёжности – это коэффициент готовности КГ. Этот показатель характеризует одновременно 2 свойства надёжности – безотказность и ремонтопригодность. Согласно ГОСТ [2] КГ определяется как вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени,кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. Математически КГ выражается формулой
КГ = Т/(Т+ТВ) (3.19)
Анализ выражения (3.19) показывает, что коэффициент готовности действительно представляет собой основной интегральный показатель качества проведения работ по эксплуатационному обслуживанию СВТ. Известно, что согласно ГОСТ [6] качество продукции – это совокупность её свойств, обусловливающих ее пригодность удовлетворять определённые потребности в соответствии с ее назначением. Аналогичным образом определим качество СВТ как совокупность её свойств, обусловливающих её пригодность удовлетворять определённые потребности в соответствии со своим назначением.
Количественную характеристику свойств объекта называют показателем его качества. Показатели качества объекта делятся на е диничные (характеризуют одно свойство объекта) и комплексные (характеризуют совокупность всех свойств объекта). В этих условиях единичными показателями СВТ будут являться, во-первых, её безотказность при некоторой системе его эксплуатационного обслуживания, во-вторых, ремонтопригодность. Количественным единичным показателем качества, характеризующим безотказность, является средняя наработка на отказ, таким же показателем, характеризующим ремонтопригодность – среднее время восстановления (т.е. всего 2 единичных показателя).
Для объединения перечисленных единичных показателей 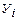 (i=1,2) в комплексном
(i=1,2) в комплексном 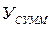 последний целесообразно представить в виде интегрального показателя качества, который ГОСТ [6] предлагает записывать как средневзвешенное значение единичных показателей
последний целесообразно представить в виде интегрального показателя качества, который ГОСТ [6] предлагает записывать как средневзвешенное значение единичных показателей 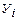 , т.е.
, т.е.
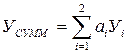 , (3.20)
, (3.20)
где 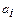 – весовой коэффициент при i -ом единичном показателе качества, определяемый методом экспертных оценок, опытом работы или социологическим опросом потребителей. Если совокупность единичных показателей
– весовой коэффициент при i -ом единичном показателе качества, определяемый методом экспертных оценок, опытом работы или социологическим опросом потребителей. Если совокупность единичных показателей 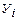 представить в виде двумерного вектора
представить в виде двумерного вектора 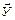 , а совокупность весовых коэффициентов
, а совокупность весовых коэффициентов 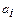 – в виде двумерного вектора
– в виде двумерного вектора 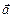 , то формулу (3.20) несложно переписать в виде скалярного произведения векторов
, то формулу (3.20) несложно переписать в виде скалярного произведения векторов 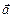 и
и 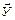 , т.е.
, т.е.
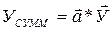 , (3.21)
, (3.21)
где «*» в (3.21) – знак скалярного произведения 2-х векторов. Однако в нашем случае, когда 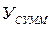 = КГ, никакие весовые коэффициенты не нужны, связь (3.19) между комплексным (интегральным) показателем качества КГ и единичными показателями Т и ТВ – строго однозначная.
= КГ, никакие весовые коэффициенты не нужны, связь (3.19) между комплексным (интегральным) показателем качества КГ и единичными показателями Т и ТВ – строго однозначная.
Физически коэффициент готовности показывает, какую долю времени восстанавливаемый объект находится в работоспособном состоянии. Например, соотношение КГ = 0,96 говорит о том, что 96 % времени объект находится в работоспособном состоянии и 4 % – в неработоспособном. Этот физический смысл широко используется в науке «Организация производства» для определения фактической производительности станка при известной его номинальной производительности и известном КГ. Пусть номинальная производительность ПН равна 500 деталей в смену, а КГ = 0,96. Тогда станок будет находиться в работоспособном состоянии только 96 % времени смены и за это время обработает 500*0,96=480 (деталей). Это и будет фактическая производительность станка ПФ, равная 480 деталей в смену. Отсюда следует взаимосвязь между фактической производительностью ПФ станка и его номинальной производительностью ПН при известном КГ
ПФ,= ПН*КГ. (3.22)
 2015-01-30
2015-01-30 4186
4186
