Следствия

·

·

·

·

Второй замечательный предел[править | править вики-текст]

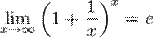или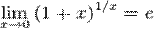

Доказательство второго замечательного предела:

Доказательство для натуральных значений x [показать]

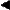Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что 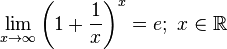. Рассмотрим два случая:

1. Пусть 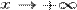. Каждое значение x заключено между двумя положительными целыми числами: 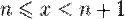, где 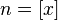— это целая часть x.

Отсюда следует: 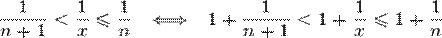, поэтому

.

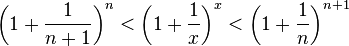Если 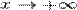, то 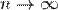. Поэтому, согласно пределу 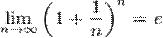, имеем:

.

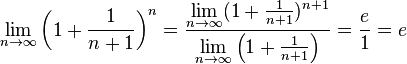
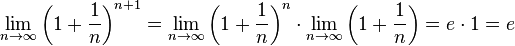По признаку (о пределе промежуточной функции) существования пределов .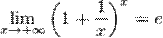

2. Пусть 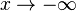. Сделаем подстановку 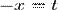, тогда

.

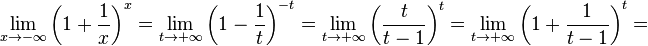
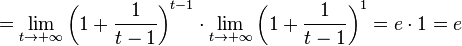Из двух этих случаев вытекает, что 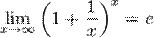для вещественного x.