взятия предела числовой последовательности является линейным, т. е. проявляет два свойства линейных отображений.
·
· Аддитивность. Предел суммы числовых последовательностей есть сумма их пределов, если каждый из них существует.
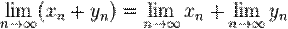
· Однородность. Константу можно выносить из-под знака предела.

· Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует.

· Предел отношения числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой.
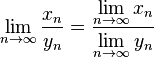
Свойства сохранения порядка [править | править вики-текст]
· Если все элементы сходящейся последовательности, начиная с некоторого номера, не превышают некоторого числа, то и предел этой последовательности также не превышает этого числа.
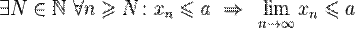
· Если некоторое число не превышает все элементы сходящейся последовательности, начиная с некоторого номера, то оно также не превышает и предела этой последовательности.
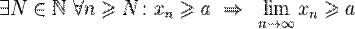
· Если некоторое число строго превышает все элементы сходящейся последовательности, начиная с некоторого номера, то предел этой последовательности не превышает этого числа.
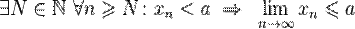
· Если все элементы сходящейся последовательности, начиная с некоторого номера, строго превышают некоторое число, то это число не превышает предела этой последовательности.
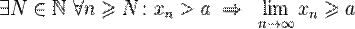
· Если, начиная с некоторого номера, все элементы одной сходящейся последовательности не превышают соответствующих элементов другой сходящейся последовательности, то и предел первой последовательности не превышает предела второй.
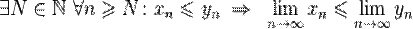
· Для числовых последовательностей справедлива теорема о двух милиционерах (принцип двустороннего ограничения).
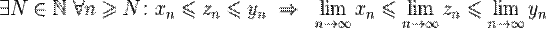
 2015-01-30
2015-01-30 2312
2312








