Смешанное произведение трех векторов

Скалярное произведение вектора 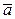на вектор 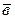, определяется соотношением:

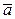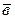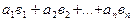× = . (11)

Например, 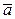× 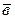= 3 * (-1) + 1 * 2 + 4 * 1 + 0 * (-4) = 3.

Свойства:

1. ;

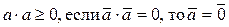2. ;

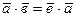3. ;

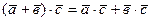4. 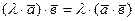. (12)

Длина вектора: 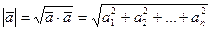. (13)

Например, .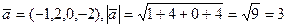

Косинус угла между векторами определяется формулой:

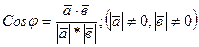. (14)

Векторы называют ортогональными, если 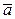* 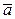= 0 (т. е. Cosj = 0).

Например, 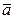= (-1, 1, 0, 1), 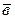= (2, -1, 1, 0);

.

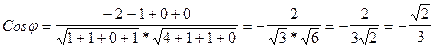Координаты вектора 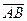вычисляются по формуле:

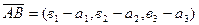, (15)

где А(а₁, а₂, а₃) и В(в₁, в₂, в₃).

Например, А(1, -3, 2), В(2, -2, 3) 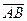= (1, 1, 1).

Проекцией вектора 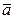на вектор 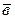называется произведение длины вектора 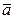на косинус угла между векторам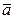и и 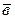, и обозначается .

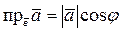Векторное произведение - это вектор, который вычисляется по формуле

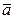= (а₁, а₂, а₃), 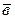= (в₁, в₂, в₃);

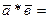
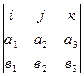. (16)

Разлагаем определитель по первой строке:

;

.

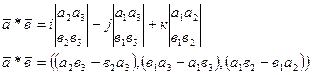
Например, 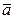= (1, -1, 0), 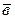= (2, -1, 1);

;

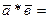
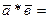(-1, -1, 1).

Свойства:

1.

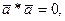
2. ,

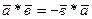3. ,

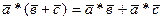4. 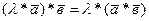. (17)

Длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.

Смешанное произведение трех векторов 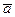= (а₁, а₂, а₃), 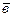= (в₁, в₂, в₃),

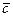= (с₁, с₂, с₃) определяется выражением: 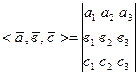. (18)

Например, 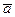= (1, -1, 0), 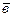= (1, 0, -1), 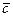= (0, 1, -1),

< , , > = .

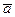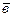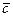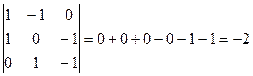Абсолютная величина смешанного произведения равна объему параллелепипеда, построенного на этих векторах.