Задача № 4. Ав и обратную к ней. Вычислим: =

Для матриц:

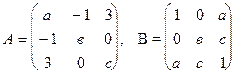, вычислить матрицу ,

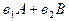АВ и обратную к ней. Вычислим: = ;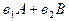

2. Вычислим: ;

3. Вычислим: .

Если çС ç¹ 0, то матрица имеет обратную.

; ; ;

; ; ;

; ;

.

4. Прямая в пространстве R²

X2

L

А(а1а2)

Общим уравнением прямой

является уравнение вида

М(х1х2)

А₁х₁ +А_2­х₂+В=0. (19)

j

X1

Если А₂ ¹0, то, разрешая (19)

относительно х₂ ­, получим

уравнение прямой с угловым коэффициентом:

. (20)

Геометрический смысл числа k состоит в том, что k = tgj, где j - угол, образованный L с положительным направлением оси ОХ₁. У перпендикулярных прямых угловые коэффициенты равны (k₁ = k₂). У перпендикулярных прямых угловые коэффициенты обратны по величине и противоположны по знаку 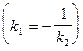. Уравнение прямой, имеющей угловой коэффициент k и проходящей через точку А(а₁, а₂), записывается в виде: х₂ - а₂ = k(х₁ - а_1­). (21)

Уравнение прямой, проходящей через две точки А(а₁, а₂) и В(в₁, в₂), имеет вид: . (22)

ЗАДАЧА № 5

Даны координаты вершин треугольника АВС: А(а, в), В(в, с), С(с, а).

Найти: 1) уравнение стороны ВС;

2) уравнение медианы АМ;

3) уравнение высоты, опущенной из вершины А.

1. Уравнение стороны ВС: .

2. Уравнение медианы АМ: найдем координаты точки М 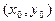: . Теперь напишем уравнение медианы АМ: .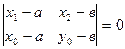

3. Уравнение высоты АН: найдем угловой коэффициент прямой ВС: .

Так как прямая ВС перпендикулярна АН, то угловой коэффициент прямой АН

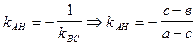. Тогда уравнение высоты имеет вид: .