Пусть 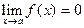 и
и 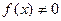 в окрестности точки а, тогда функция
в окрестности точки а, тогда функция 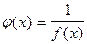 называется бесконечно большой функцией. Обозначается
называется бесконечно большой функцией. Обозначается 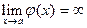 .
.
Если функция f(x) - бесконечно большая и f(x)¹ 0 в окрестности точки а, то 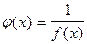 - бесконечно малая функция. Условные обозначения:
- бесконечно малая функция. Условные обозначения: 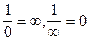 .
.
Как понимать х ® + ¥, х ® - ¥ и х ® ¥? Будем говорить, что х ® + ¥, если х может стать больше любого наперед заданного числа, х ® - ¥, если х может стать меньше любого наперед заданного числа, х ® ¥, если абсолютная величина х может стать больше любого наперед заданного числа.
Например, 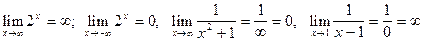 .
.
Свойства пределов:
1. Предел суммы функций, состоящий из конечного числа слагаемых, равен сумме пределов.
2. Предел произведения равен произведению пределов.
3. Предел частного равен частному пределов, если предел знаменателя неравен нулю.
Например, если 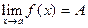 и
и 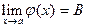 , то
, то
а) 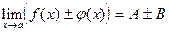 ;
;
б) 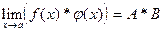 ;
;
в) 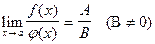 .
.
Неопределенности. Неопределенность 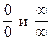
Рассмотрим вычисление 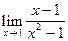 . Подставим вместо х предельное значение 1:
. Подставим вместо х предельное значение 1: 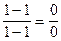 . Эта ситуация называется неопределенностью
. Эта ситуация называется неопределенностью 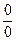 . Для того, чтобы вычислить
. Для того, чтобы вычислить 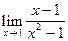 , разложим знаменатель на множители
, разложим знаменатель на множители
х2-1=(х-1)*(х+1), и подставим в выражение 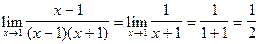 .
.
Рассмотрим вычисление 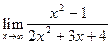 . При стремлении х к бесконечности, многочлены в числителе и знаменателе стремятся к бесконечности, и возникает неопределенность вида
. При стремлении х к бесконечности, многочлены в числителе и знаменателе стремятся к бесконечности, и возникает неопределенность вида 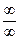 . Для того, чтобы вычислить
. Для того, чтобы вычислить 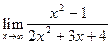 , вынесем х2 в числителе и знаменателе за скобки
, вынесем х2 в числителе и знаменателе за скобки
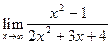 =
= 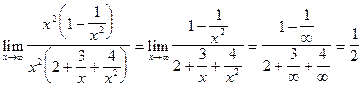 .
.
 2015-01-30
2015-01-30 462
462








