2015-01-30
686
Пример 1. Уравнение движения материальной точки вдоль оси имеет вид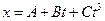 
, где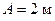 
, 
, 
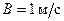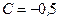м/с3. Найти координату x, проекции скорости v х и ускорения a х точки в момент времени 
.
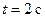Решение. Координату x найдем, подставив в уравнение движения числовые значения коэффициентов A, B и C и времени t:
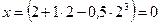м.
Проекция мгновенной скорости есть первая производная от координаты по времени
.
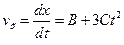В момент времени 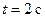проекция скорости
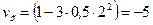м/с.
Проекция ускорения - первая производная от проекции скорости по времени
.
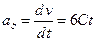В момент времени 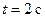проекция ускорения
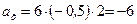м/с2.
Ответ: 
м/с.
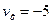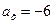м/с2.
Пример 2. Тело вращается вокруг неподвижной оси по закону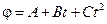 
, где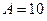 
рад,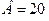 
рад/с, 
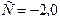рад/с2. Найти полное ускорение точки, находящейся на расстоянии 
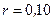м от оси вращения, для момента времени 
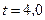с.
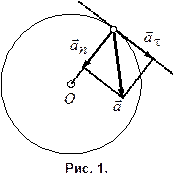Решение. Полное ускорение 
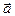точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения 
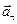, направленного по касательной к траектории, и нормального ускорения 
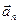, направленного к центру кривизны траектории (рис. 1):
.
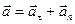Векторы 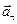и 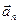взаимно перпендикулярны, поэтому полное ускорение равно
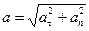. (1)
Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами:
, 
,
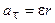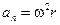где w - угловая скорость тела, e - его угловое ускорение.
Подставляя выражения для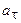 
и 
в формулу (1), находим:
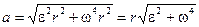. (2)
Угловую скорость w найдем, взяв производную угла поворота по времени:
.
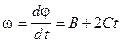В момент времени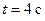 
угловая скорость
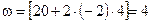рад/с.
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:
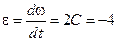рад/с2.
Это выражение не содержит времени, следовательно, угловое ускорение заданного движения постоянно. Подставляя найденные значения w и e, а заданное значение r в формулу (2), получим
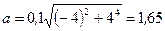м/с2.
Ответ: 
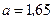м/с2.
Пример 3. Ящик массой 
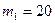кг соскальзывает по идеально гладкому лотку длиной 
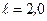м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой 
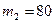кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении. Определить скорость u тележки с ящиком, если лоток наклонен под углом 
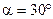к рельсам.
Решение. Тележку и ящик можно рассматривать как систему двух неупруго взаимодействующих тел.
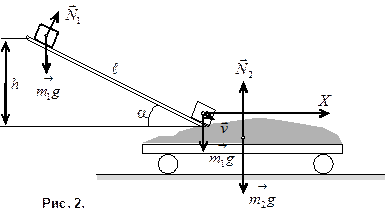
Эта система не замкнутая, т.к. сумма внешних сил, действующая на систему: двух сил тяжест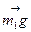и 
и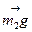 
и силы реакции 
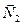(рис. 2), не равна нулю. Поэтому применить закон сохранения импульса к системе ящик-тележка нельзя. Но так как проекция суммы указанных сил на направление оси x, совпадающей с направлением рельсов, равна нулю, то составляющую импульса системы в этом направлении можно считать постоянной, т.е.
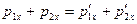, (1)
где 
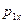и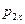 
- проекции импульса ящика и тележки с песком в момент падения ящика на тележку; 
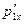и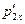 
- те же величины после падения ящика.
Выразим в равенстве (1) импульсы тел через их массы и скорости, учитывая, что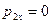 
(тележка до взаимодействия с ящиком покоилась), а также, что после взаимодействия оба тела системы движутся с одной и той же скоростью u:
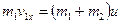
или
,
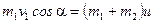где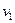 
- скорость ящика перед падением на тележку; 
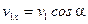- проекция этой скорости на ось x.
Отсюда выразим искомую скорость:
.
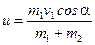Скорость 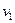определим из закона сохранения энергии:
.
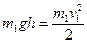где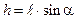 
. После сокращения 
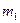найдем
.
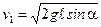Подставив найденное выражение 
в формулу (2), получим
.
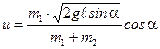Подставим сюда числовые значения величин и произведем вычисления:
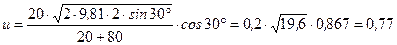м/с.
Ответ: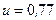 
м/с.
Пример 4. Шар массой 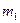, движущийся горизонтально с некоторой скоростью 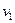, столкнулся с неподвижным шаром массой 
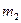. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?
Решение. Доля e энергии, переданной первым шаром второму, выразится соотношением:
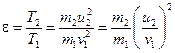. (1)
где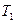 
- кинетическая энергия первого шара до удара; 
и 
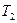- скорость и кинетическая энергия второго шара после удара.
Как видно из формулы (1), для определения e надо найти .
При ударе абсолютно упругих тел одновременно выполняются два закона сохранения: закон сохранения импульса и закон сохранения механической энергии. Пользуясь этими законами, найдем . По закону сохранения импульса, учитывая, что второй шар до удара покоился, получим
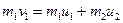. (2)
По закону механической энергии
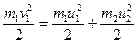. (3)
Решая совместно уравнения (2) и (3), найдем
.
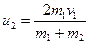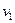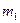Подставив это выражение для в формулу (1) и сократив на и , получим
.
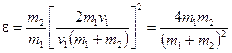Из полученного соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров. Доля передаваемой энергии не изменится, если шары поменяются местами.
Ответ: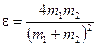 
.
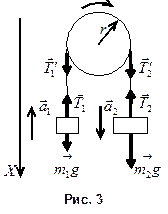Пример 5. Через блок в виде сплошного диска, имеющего массу 
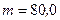г (рис. 3), перекинута тонкая, гибкая нить, к концам которой подвешены грузы с массами 
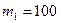г и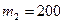 
г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением и массой нити пренебречь.
Решение. Воспользуемся основными уравнениями динамики поступательного и вращательного движений. Для этого рассмотрим силы, действующие на каждый груз в отдельности и на блок. На первый груз действуют две силы: сила тяжести 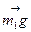и сила упругости (сила натяжения нити) 
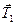. Спроектируем эти силы на ось x, которую направим вертикально вниз, и напишем уравнение движения (второй закон Ньютона) в координатной форме:
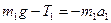. (1)
Уравнение движения для второго груза запишется аналогично:
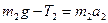. (2)
Учтем, что модули ускорений тел одинаковые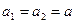 
, поскольку нить невесомая и нерастяжимая.
Под действием двух моментов сил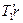 
и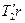 
относительно оси, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение e 
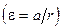. Согласно основному уравнению динамики вращательного движения
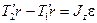. (3)
где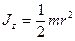 
- момент инерции блока (сплошного диска) относительно оси z, которая направлена за чертеж.
Сила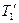 
согласно третьему закону Ньютона по абсолютному значению равна силе 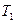. Соответственно сила 
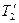по абсолютному значению равна силе 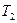. Воспользовавшись этим, подставим в уравнение (3) вместо 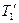и 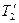выражения для 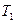и 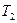, получив их предварительно из уравнений (1) и (2):
.
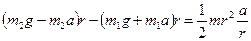После сокращения на r и перегруппировки членов найдем интересующее нас ускорение:
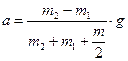. (4)
Отношение масс в правой части формулы (4) есть величина безразмерная. Поэтому массы 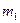, 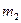и m можно выразить в граммах, как они даны в условии задачи. Ускорение g надо выразить в единицах СИ. После подстановки получим:
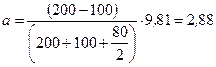м/с2.
Ответ: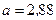 
м/с2.
