Биномиальным наз-ся распределение сл\в, в кот она принимает последовательность целых неотрицательных значений с вер-ми определяемыми по формуле Бернулли. 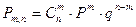
мат\о 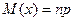 и дисперсия
и дисперсия 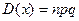 биномиально распределённой сл\величины.
биномиально распределённой сл\величины.
Законом распределения Пуассона наз распр-е сл\в, в кот она принимает последовательность целых неотрицательных значений с вер-ми определ-ся по формуле Пуассона. Если имеет место распределение Пуассона заданного распр-я 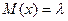 , то мат\о находится
, то мат\о находится 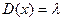
Распределение Пуассона. Пусть производится n независимых испытаний, в кот появление соб А имеет в-ть р. Если число испытаний n достаточно велико, а в-ть появления соб А в каждом испытании мало, то для нахождения в-ти появления события А k раз находится след образом: Произведение np сохраняет постоянное значение:  , это означает, что среднее число появления соб в различных сериях испытаний (при разном n) остается неизменным.
, это означает, что среднее число появления соб в различных сериях испытаний (при разном n) остается неизменным.
По формуле Бернулли получаем:
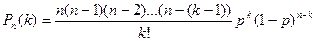 ;
; 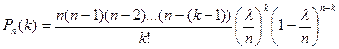
Найдем предел этой вероятности при n à ∞.
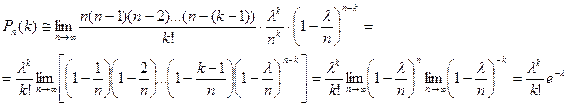
Получаем формулу распределения Пуассона: 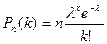
 2015-01-30
2015-01-30 1412
1412
