Сл\в Х наз-ся непрерывной, если её Функция Распределения непрерывна в любой точке и дифференцируемая во всюду, кроме отдельных точек (точки излома).
Мат\ожиданием дискретной сл\в называется сумма произведений всех возможных значений сл\в на их вероятности.
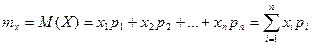 Мат\о существует, если ряд, стоящий в правой части равенства, сходится абсолютно. С точки зрения вер-ти можно сказать, что м\о приближенно = среднему арифметическому наблюдаемых значений сл\в.
Мат\о существует, если ряд, стоящий в правой части равенства, сходится абсолютно. С точки зрения вер-ти можно сказать, что м\о приближенно = среднему арифметическому наблюдаемых значений сл\в.
Пусть НСВ Х задана ФР F(x). Допустим, что все возможные значения сл\в принадлежат отрезку [a,b].
Мат\ож-м НСВ Х, возможные значения которой принадлежат отрезку [a,b], наз-ся определенный интеграл 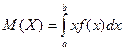 . Если возможные значения сл\в рассм-ся на всей числовой оси, то мат\о нах по формуле:
. Если возможные значения сл\в рассм-ся на всей числовой оси, то мат\о нах по формуле: 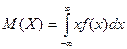 , при этом предпол-ся, что несобственный интеграл сходится.
, при этом предпол-ся, что несобственный интеграл сходится.
Дисперсией НСВ наз мат\ож квадрата ее отклонения. 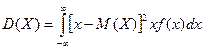 . По аналогии с дисперсией, дискретной сл\в, для практического вычисления дисперсии используется формула:
. По аналогии с дисперсией, дискретной сл\в, для практического вычисления дисперсии используется формула: 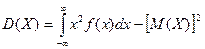 .
.
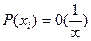 , в качестве способа задания НСВ используется функция распределения НСВ.
, в качестве способа задания НСВ используется функция распределения НСВ.
ФРНСВ наз вер-ть т\ч она примет значение меньшее заданного. 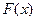 -обознач ф-ии распр в-тей
-обознач ф-ии распр в-тей
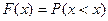 à
à 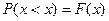
Основные свойства ф-ии распределения НСВ:
С1. 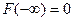
С2. 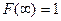
С3. 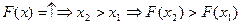
С4. Вер-ть т\ч НСВ примет значение из интервала, равна приращению ф-ии на этом интервале 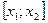
1) 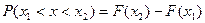

2) 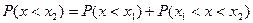
Плотность вероятности НепрерывныхСВ, её определение, свойства. Кривая распределения. Связь между функцией распределения и плотностью вероятности НСВ. Математическое ожидание и дисперсия НСВ.
Скорость изменения функции распределения хар-ся плотностью распр-я. Обозначается символом 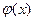 . Плотностью вер-ти (плотностью распр-я)
. Плотностью вер-ти (плотностью распр-я) 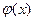 НСВ Х наз-ся производная её ф-ии распр-я
НСВ Х наз-ся производная её ф-ии распр-я 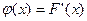
Свойства плотности распр-я (ПР):
С1. ПР – неотрицательная функция. 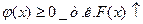 ;
;
С2. Вер-ть попадания НСВ в интервал [a,b] равна определённому интегралу от её плотности вер-ти в пределах от a до b, т.е. 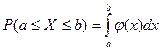
С3. Ф-я распр НСВ м\б выражена через плотность вер-ти по формуле: 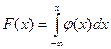
С4. Несобственный интеграл в бесконечных пределах от плотности вер-ти НСВ =1. 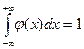
Из выражений, связывающих плотность и функцию распределения следует, что м\у ними существует взаимно однозначное соответствие, те каждое из них определяет выражение другой.
Плотность вер-ти, как и ф-ция рапр-я явл-ся одной из форм закона распределения, но в отличии от ф-ции рапр, она существует только для НСВ. Плотность вер-ти называют и дифференциальной функцией. График плотности вер-ти называется кривой распределения.
ПР составляет основания определения хар-к сл\в: мат\о и дисперсии.
Мат\ожиданием НСВ Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл 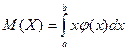 . Если возможные значения сл\в рассматриваются на всей числовой оси, то м\о находится по формуле:
. Если возможные значения сл\в рассматриваются на всей числовой оси, то м\о находится по формуле: 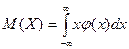 . При этом предполагается, что несобственный интеграл сходится.
. При этом предполагается, что несобственный интеграл сходится.
Дисперсией НСВ называется мат\о квадрата ее отклонения. 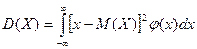
По аналогии с дисперсией дискретной сл\в, для практического вычисления дисперсии используется формула: 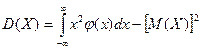
Мат\о определяется: 
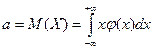 ,если интеграл абсолютно сходится и
,если интеграл абсолютно сходится и 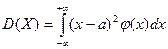 , если интеграл сходится. С3 дисперсии имеет вид:
, если интеграл сходится. С3 дисперсии имеет вид: 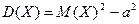 или
или 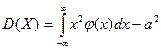
 2015-01-30
2015-01-30 5311
5311
