Предположим, что событие А может произойти при условии появления одного из несовместных событий (гипотез) Hi, известны вероятности этих гипотез р(Hi) и условные вероятностир(А| Hi). Дополнительно известно, что событие А произошло. Найдем вероятность того, что при этом была реализована гипотеза Hk. По определению условной вероятности
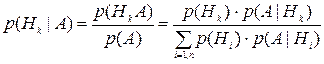 (1.36)
(1.36)
Полученное соотношение называют формулой Байеса. Она позволяет по известным (до проведения опыта) априорным вероятностям гипотез р(Нi) и условным вероятностям р(А| Hi) определить условную вероятность р(Hi | А), которую называют апостериорной (то есть полученной при условии, что в результате опыта событие А уже произошло).
Пример 1.63. 30% пациентов, поступающих в больницу, принадлежат первой социальной группе, 20% – второй и 50% - третьей. Вероятность заболевания туберкулезом для представителя каждой социальной группы, соответственно, равна 0,02, 0,03 и 0,01. Проведенные анализы для случайно выбранного пациента показали наличие туберкулеза. Найти вероятность того, что это представитель третьей группы.
Решение. Пусть Н1, Н2, Н3 – гипотезы, заключающиеся в том, что пациент принадлежит соответственно первой, второй и третьей группам. Очевидно, что они образуют полную группу событий, причем р(Н1)=0,3, р(Н2)=0,2, р(Н3)=0,5. По условию событие А, обнаружение туберкулеза у больного, произошло, причем условные вероятности по данным условия равны Р(А| H1)=0,02, Р(А| H2)=0,03 и Р(А| H3)=0,01. Апостериорную вероятность Р(H3 | А) вычислим по формуле Байеса:
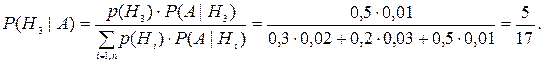
12. Повторение испытаний: формула Бернулли; асимптотическая формула Муавра-Лапласа; Интегральная теорема Лапласа; распределение Пуассона.
Формула Бернулли (Якоб Бернулли, 1654-1705)
При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых возникает необходимость определения параметров случайных событий при многократном повторении одного и того же опыта или аналогичных опытов при неизменном комплексе условий. В результате каждого опыта может появиться или не появиться некоторое событие А, причем нас интересует не результат каждого отдельного опыта, а общее число появлений события А в результате серии опытов. Например, общее число попаданий в серии выстрелов по одной и той же цели. В подобных задачах требуется определять вероятность любого заданного числа появлений события в результате серии опытов. Такие задачи весьма просто решаются в случае, когда опыты являются независимыми.
Несколько опытов называются независимыми относительно события А, если вероятность появления события А в каждом испытании не зависит от исходов других испытаний. Например, бросание монеты – независимые опыты. Вынимание нескольких карт из колоды представляют независимые опыты, если карты возвращаются в колоду.
В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность. Будем далее рассматривать лишь такие независимые испытания, в которых событие А имеет одну и ту же вероятность.
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться, либо не появиться. Пусть вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q =1‑p. Если каждое отдельное испытание рассматривается как простое событие, то событие, состоящее из совокупности таких простых событий, называется сложным событием. Например, вероятность того, что в четырех испытаниях событие А появится 3 раза, можно представить в виде следующих сложных событий: ААА 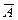 , АА
, АА 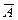 А, А
А, А 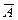 АА,
АА, 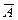 ААА. Такие случайные события описываются схемой Бернулли.
ААА. Такие случайные события описываются схемой Бернулли.
Схемой Бернулли называется последовательность испытаний, удовлетворяющая следующим условиям:
1) при каждом испытании различают лишь два исхода: появление события А, называемый «успехом», либо не появление события А («неуспех»);
2) испытания являются независимыми, то есть, исход каждого испытания не зависит от исходов всех предыдущих испытаний;
3) вероятность появления события А во всех испытаниях постоянна и равна Р(А) = р, вероятность противоположного события – не появления события А также постоянна и равна Р(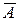 ) = 1 – р =q
) = 1 – р =q
Поставим перед собой задачу: определить вероятность того, что при n испытаниях событие А появится ровно k раз и, следовательно, не появится n-k раз. Искомую вероятность обозначают Рn(k). По теореме умножения вероятностей независимых событий (формула (1.28)) эта вероятность равна Рn(k) = pk ∙qn-k. Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т.е. 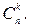 Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий (аксиома 4) искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления события А ровно k раз в n событиях) равна вероятности одного сложного события, умноженной на их число:
Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий (аксиома 4) искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления события А ровно k раз в n событиях) равна вероятности одного сложного события, умноженной на их число:
Рn(k) = 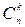 pk ∙qn-k
pk ∙qn-k
или 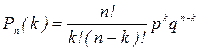 (1.37)
(1.37)
Полученную формулу называют формулой Бернулли или биномиальной формулой Бернулли.
 2015-01-30
2015-01-30 1956
1956
