Локальная теорема Лапласа. Асимптотическая

формула Муавра-Лапласа (Пьер Симон Лаплас, 1749-1827)

(Абрахам де Муавр, 1667-1754)

При больших значениях n, k, p (0<р<1) пользоваться формулой Бернулли достаточно трудно, так как формула требует выполнения действий над громадными числами. Например, если n=50, k=30, p=0,1, то для отыскания вероятности Р₅₀(30) надо вычислить выражение

Р₅₀(30)= 50!/(30!20!)∙(0,1)³⁰∙(0,9)²⁰,

где 50! = 30 414 093∙10⁵⁷, 30! = 26 525 286∙10²⁵ , 20!= 24 329 020∙10¹¹ .

Оказывается можно упростить процесс вычисления интересующей нас вероятности.

Если число испытаний n достаточно велико, вероятность появления события А ровно k раз в n испытаниях можно найти по теореме Лапласа и асимптотической формуле Муавра-Лапласа.

Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р _n(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n) значению функции

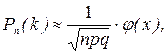(1.39)

где 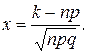- функция Гаусса.

Значения функции φ(х) приводятся в специальных таблицах (например, Гмурман, приложение 1) для положительных значений х. Для отрицательных значений х можно пользоваться теми же таблицами, так как функция φ(х) нечетна, т.е. φ(-х)= -φ(х).

Пример 1.67. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.

Решение. По условию n=400; k=80; p=0,2; q=0,8. по асимптотической формуле Муавра-Лапласа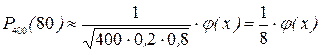

Вычислим определяемое данными задачи значение х:

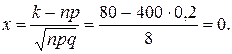
По таблице приложения 1 (Гмурман В.Е.) находим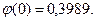

Искомая вероятность Р₄₀₀(80)=(1/8)∙0,3989=0,04986.

Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости упущены): Р₄₀₀(80)=0,0498.