2015-01-30
1429
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений события А в этих испытаниях используется формула Бернулли. Если же n велико, то пользуются асимптотической формулой Муавра-Лапласа. Однако, эта формула непригодна, если вероятность события мала (р≤0,1). В этих случаях (n велико, р мало, а их произведение np<10) прибегают к асимптотической формуле Пуассона.
Сделаем допущение: произведение np сохраняет постоянное значение, то есть np=λ=сonst. Это означает, среднее число появлений события А в различных сериях испытаний, т.е. при различных значениях n, остается неизменным.
По формуле Бернулли интересующая нас вероятность равна
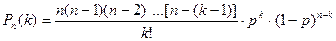
Так как np=λ, то p= λ/n. Следовательно,
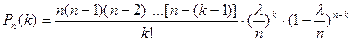
Так как n имеет очень большое значение, вместо Рn(k) найдем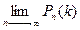 
. При этом будет найдено лишь приближенное значение отыскиваемой вероятности: хотя n и велико, но конечно при отыскании предела мы устремим n к бесконечности. Поскольку произведение np сохраняет свое постоянное значение, то при n→ ∞ вероятность р→0.
Итак,
Таким образом,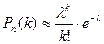 
(1.41)
Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) и редких (p мало) событий. Имеются специальные таблицы, пользуясь которыми можно найти Pn(k), зная k и λ.
13. Случайные величины: дискретные и непрерывные случайные величины. Функция распределения дискретной случайной величины и её свойства.
Основные определения. Результат любого случайного эксперимента можно характеризовать качественно и количественно. Качественный результат случайного эксперимента - случайноесобытие. Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества значений, - случайная величина. Случайная величинаявляется одним из центральных понятий теории вероятностей.
Пусть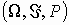 
- произвольное вероятностное пространство. Случайной величиной называется действительная числовая функция x =x (w), w 
W, такая, что при любом действительном x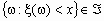 
.
Событие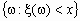 
принято записывать в виде x < x. В дальнейшем случайные величины будем обозначать строчными греческими буквами x, h, z, …
Случайной величиной является число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента. В первом случае мы имеем дело с дискретнойслучайной величиной (она принимает значения из дискретного числового множества M= {1, 2, 3, 4, 5, 6}; во втором случае - с непрерывной случайной величиной (она принимает значения из непрерывного числового множества - из промежутка числовой прямой I =[100, 3000]).
Функция распределения случайной величины. Её свойства
Каждая случайная величина полностью определяется своей функцией распределения.
Если x.- случайная величина, то функция F (x) = Fx (x) = P (x < x) называется функцией распределения случайной величины x. Здесь P (x < x) - вероятность того, что случайная величина xпринимает значение, меньшее x.
Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.
Функция распределения любой случайной величины обладает следующими свойствами:
· F (x)определена на всей числовой прямой R;
· F (x)не убывает, т.е. если x 1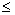 
x 2, то F (x 1) 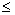F (x 2);
· F (-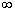 
)=0, F (+ 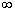)=1,т.е. 
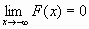и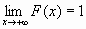 
;
· F (x) непрерывна справа, т.е.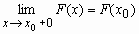 
.
Функция распределения дискретной случайной величины
Если x - дискретная случайная величина, принимающая значения x 1 < x 2 < … < xi < … с вероятностями p 1 < p 2 < … < pi < …, то таблица вида
| x 1 | x 2 | … | xi | … |
| p 1 | p 2 | … | pi | … |
называется распределением дискретной случайной величины.
Функция распределения случайной величины, с таким распределением, имеет вид
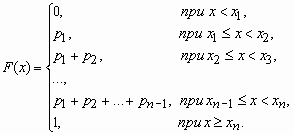
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
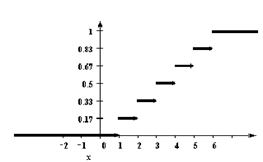
Функция распределения и плотность вероятности непрерывной случайной величины
Если функция распределения Fx (x) непрерывна, то случайная величина x называется непрерывной случайной величиной.
Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины px (x), которая связана с функцией распределения Fx (x) формулам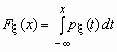и
и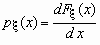 
.
Отсюда, в частности, следует, что для любой случайной величины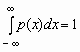 
.
Квантили
При решении практических задач часто требуется найти значение x, при котором функция распределения Fx (x) случайной величины x принимает заданное значение p, т.е. требуется решить уравнение Fx (x) = p. Решения такого уравнения (соответствующие значения x) в теории вероятностей называются квантилями.
Квантилью xp (p -квантилью, квантилью уровня p) случайной величины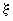 
, имеющей функцию распределения Fx (x), называют решение xp уравнения Fx (x) = p, p (0, 1). Для некоторых p уравнение Fx (x) = p может иметь несколько решений, для некоторых - ни одного. Это означает, что для соответствующей случайной величины некоторые квантили определены неоднозначно, а некоторые кванитили не существуют.
Квантили, наиболее часто встречающиеся в практических задачах, имеют свои названия:
медиана - квантиль уровня0.5;
нижняя квартиль - квантиль уровня0.25;
верхняя квартиль - квантиль уровня0.75;
децили - квантили уровней0.1, 0.2, …, 0.9;
процентили - квантили уровней 0.01, 0.02, …, 0.99.
Вероятность попадания в интервал
Вероятность того, что значение случайной величины Fx (x) попадает в интервал (a, b), равная P (a <x < b) = Fx (b) - Fx (a), вычисляется по формулам:
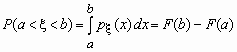- для непрерывной случайной величины и
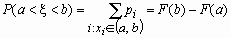- для дискретной случайной величины.
Если a= - 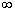, то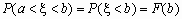 
,
если b= 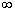, то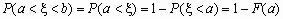 
.
14. Числовые характеристики случайной величины: математическое ожидание дискретных и непрерывных случайных величин; свойства математического ожидания.
Закон распределения случайной величины дает исчерпывающую информацию о случайной величине. Однако, иногда можно охарактеризовать достаточно ярко случайную величину с помощью всего одного или нескольких чисел. Например, можно указать закон распределения количества осадков выпадающих в данной местности за определенный месяц, но проще инагляднее указать среднее количество осадков в данном месяце.
Числа, назначение которых в сжатом виде характеризовать основные особенности распределений случайных величин, называются числовыми характеристиками. Рассмотрим некоторые из числовых характеристик и их основные свойства.
