Дисперсия обладает следующими свойствами

1. Если случайная величина состоит из одной тотчки 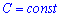— постоянная величина, то дисперсия равна нулю

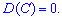
2. Дисперсия от произведения постоянной на случайную величину равна квадрату постоянной умноженной на дисперсию случайной величины

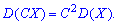
3. Если 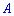и — постоянные величины, то для дисперсии 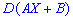справедлива зависимость

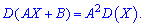
Это следует из двух предыдущих свойств.

Дисперсию можно вычислить по упрощенной формуле:

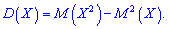
которая в случае дискретной случайной величины 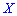имеет вид

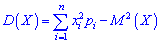
для непрерывной определяется зависимостью

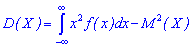
и для непрерывной на промежутке 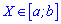соотношением

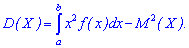
Приведенные формулы очень удобны в вычислениях, и их, в отличие от предыдущих, используют в обучении

Также следует помнить, что дисперсия всегда принимает неотрицательные значения 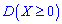. Она характеризует рассеяние случайной величины относительно своего математического ожидания. Если случайная величина измерена в некоторых единицах, то дисперсия будет измеряться в этих же единицах, но в квадрате.

Для сравнения удобно пользоваться числовыми характеристиками одинаковой размерности случайной величиной. Для этого вводят в рассмотрение среднее квадратичное отклонение – корень квадратный из дисперсии. Ее обозначают греческой буквой «сигма»

----------------------------------------

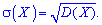
16. Непрерывные случайные величины. Плотность распределения вероятности непрерывной случайной величины, её свойства и связь с функцией распределения, математическое ожидание и дисперсия непрерывной случайной величины.