Свойства плотности вероятности

1. Функция .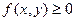

2. .

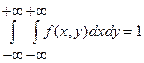3. ,

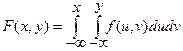где 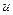и 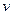- переменные интегрирования.

4.

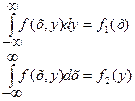
Математическим ожиданием двумерной случайной величины 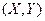называется совокупность двух математических ожиданий М[Х], М[Y], то есть упорядоченных пар М[Х], М[Y], которые определяются равенствами:

а) если Х и Y – дискретные случайные величины:

М[Х]=, : ; .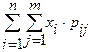

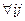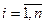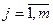М[Y]=.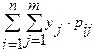

б) если Х и Y – непрерывные случайные величины:

М[Х]=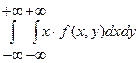

М[Y]= ,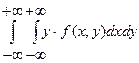

где 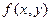- плотность вероятности двумерной случайной величины .

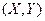Математическое ожиданиеслучайной величины 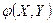, которая является функцией компонент 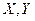двумерной случайной величины 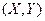, находится аналогично по формулам:

1) М[j(Х, Y)]= 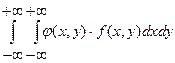- если Х и Y – непрерывные случайные величины;

2) М[j(Х, Y)]=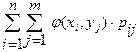, 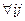: 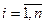; 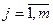- если Х и Y – дискретные случайные величины.

25. Корреляционный момент и коэффициент корреляции двух случайных величин. Коррелированность и зависимость случайных величин.

Для двумерной случайной величины 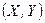характеристики ее составляющих 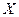и 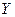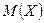, , 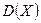, 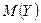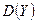никак не отражают зависимости между 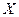и 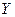или ее отсутствия. Поэтому вводится еще одна числовая характеристика − корреляционный момент или ковариация.

Определение. Ковариацией или корреляционным моментом 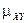случайных величин 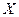и 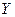называется математическое ожидание произведения отклонений этих величин от их математических ожиданий:

.

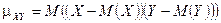Используя формулы для математических ожиданий, получаем

для дискретных величин ,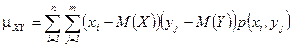

для непрерывных величин .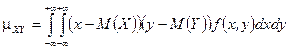

Ковариация характеризует зависимость величин.

Свойства корреляционного момента

1. Для независимых случайных величин 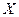и .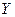

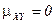2. Если 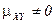, то случайные величины 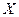и 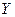зависимы.

3. 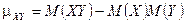. (Для доказательства достаточно раскрыть скобки под знаком математического ожидания в определении.) В частности

для дискретных величин ,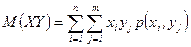

для непрерывных величин .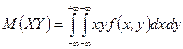

4. 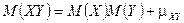. (Свойство сразу вытекает из 3.)

5. 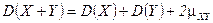. (Выразите дисперсию через математические ожидания.)

6. .

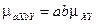7. 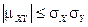. (Доказательство этого свойства можно найти в [1, гл.14, § 17].)

Ковариация имеет размерность произведения размерностей случайных величин 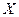и 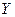и зависит от того, в каких единицах измерялись величины. Для получения безразмерной характеристики вводится понятие коэффициента корреляции.

Определение. Коэффициентом корреляции 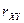случайных величин 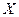и 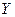называется отношение корреляционного момента к произведению средних квадратических отклонений этих случайных величин:

.

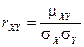Свойства коэффициента корреляции

1. Для независимых случайных величин 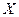и .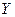

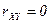2. 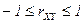. Коэффициент корреляции по абсолютной величине не превосходит единицы.

3. Если 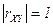, то случайные величины 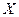и 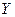связаны линейной зависимостью, т.е. .

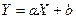Определение. Случайные величины 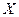и 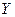называются некоррелированными, если 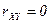, и коррелированными, если .

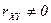Следует помнить, что понятия некоррелированности и независимости не совпадают, несмотря на внешнее сходство. Независимые величины − некоррелированные, но обратное неверно. Коррелированные величины − зависимые, но обратное неверно. Любые коррелированные величины всегда зависимые, любые независимые величины всегда некоррелированные. Это можно отразить на двудольном графе.

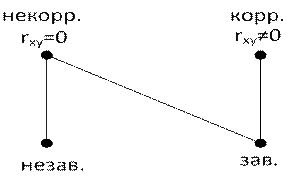
Пример. У случайных величин и 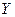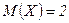, , 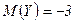, , 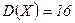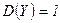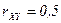. Найдите 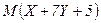и .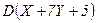

Решение. .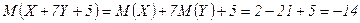

.

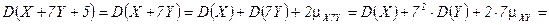
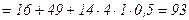Ответ. , .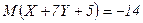

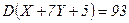В заключение рассмотрим пример на вычисление всех характеристик системы случайных величин. Этот же пример рассмотрен в заданиях 6. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН.