2015-01-30
1846
Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины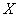 
, подчиненной нормальному закону с параметрами 
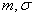, на участок от 
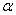до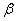 
. Для вычисления этой вероятности воспользуемся общей формулой
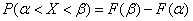, (6.3.1)
где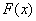 
- функция распределения величины .
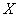Найдем функцию распределения 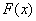случайной величины 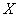, распределенной по нормальному закону с параметрами 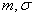. Плотность распределения величины 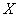равна:
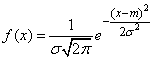. (6.3.2)
Отсюда находим функцию распределения
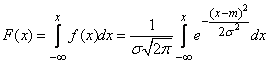. (6.3.3)
Сделаем в интеграле (6.3.3) замену переменной
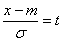
и приведем его к виду:
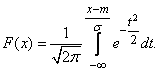(6.3.4)
Интеграл (6.3.4) не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения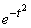 
или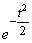 
(так называемый интеграл вероятностей), для которого составлены таблицы. Существует много разновидностей таких функций, например:
; 
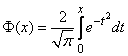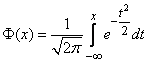
и т.д. Какой из этих функций пользоваться – вопрос вкуса. Мы выберем в качестве такой функции
|
|
|
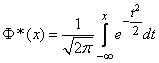. (6.3.5)
Нетрудно видеть, что эта функция представляет собой не что иное, как функцию распределения для нормально распределенной случайной величины с параметрами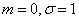 
.
Условимся называть функцию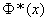 
нормальной функцией распределения. В приложении (табл. 1) приведены таблицы значений функции .
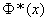Выразим функцию распределения (6.3.3) величины 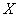с параметрам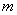и 
и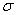 
через нормальную функцию распределения 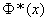. Очевидно,
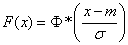. (6.3.6)
Теперь найдем вероятность попадания случайной величины 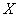на участок от 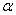до 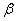. Согласно формуле (6.3.1)
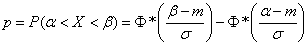. (6.3.7)
Таким образом, мы выразили вероятность попадания на участок случайной величины 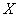, распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения 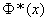, соответствующую простейшему нормальному закону с параметрами 0,1. Заметим, что аргументы функции 
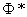в формуле (6.3.7) имеют очень простой смысл: 
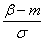есть расстояние от правого конца участка 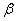до центра рассеивания, выраженное в средних квадратических отклонениях; 
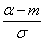- такое же расстояние для левого конца участка, причем это расстояние считается положительным, если конец расположен справа от центра рассеивания, и отрицательным, если слева.
Как и всякая функция распределения, функция 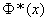обладает свойствами:
1. 
.
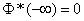2. 
.
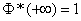3. 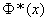- неубывающая функция.
Кроме того, из симметричности нормального распределения с параметрами 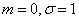относительно начала координат следует, что
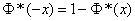. (6.3.8)
21. Система нескольких случайных величин. Закон распределения вероятностей дискретной двумерной случайной величины.
Система двух случайных величин (двумерная случайная величина) - совокупность двух совместно рассматриваемых случайных величин (X, Y).
|
|
|
Систему двух случайных величин геометрически можно интерпретировать как случайную точку с координатами (X, Y) на плоскости либо как случайный вектор, направленный из начала координат в точку (X, Y).
Целесообразно различать системы дискретных и непрерывных случайных величин, составляющие которых дискретны и непрерывны соответственно.
Закон распределения вероятностей двумерной случайной величины - соответствие между возможными значениями и их вероятностями.
Закон распределения дискретной двумерной случайной величины обычно задают в виде таблицы с указанием пары чисел (x i, y j) и их вероятностей p(x i, y j), где i = 1, 2, …, n; j = 1, 2, …, m.
Закон распределения может быть задан аналитически, в виде функции распределения.
Законом распределения дискретной двумерной случайной величины называют перечень возможных значений этой величины, т. е. пар чисел и их вероятностей p. Обычнозакон распределения задают в виде таблицы.
Первая строка таблицы содержит все возможные значения составляющей Y, а первый столбец — все возможные значения составляющей X. В клетке, стоящей на пересечении i -ой строки и j -го столбца указана вероятность того, что случайная величина примет значение:
| X | Y | |||
| y1 | y2 | … | yn | |
| x1 | p(x1,y1) | p(x1,y2) | … | p(x1,yn) |
| x2 | p(x2,y1) | p(x2,y2) | … | p(x2,yn) |
| … | … | … | … | … |
| xm | p(xm,y1) | p(xm,y2) | … | p(xm,yn) |
Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих: вероятность того, что X примет значение равна сумме вероятностей «строки». Аналогично и для других значений x.
Т.е. имеем
и т.д.
Аналогично сложив вероятности «столбца», получим вероятность того, что случайная величина
Замечание. Сумма вероятностей всех клеток таблицы закона распределения равна 1, т.е.
.
Пример
Найти законы распределения составляющих двумерной случайной величины, заданной законом распределения в табличной форме:
| X | Y | |
| y1 | Y2 | |
| x1 | 0.1 | 0.06 |
| x2 | 0.3 | 0.18 |
| x3 | 0.2 | 0.16 |
Сложив вероятности по столбцам, получим вероятности возможных значений Y: Тогда закон распределения составляющей Y имеет вид:
| Y | y1 | y2 |
| р | 0.6 | 0.4 |
Аналогично можно получить для X:
| X | x1 | x2 | x3 |
| р | 0.16 | 0.48 | 0.36 |
Замечание. Сумма вероятностей во второй строке каждой полученной таблицы равна 1.
22. Функция распределения двумерной случайной величины и её свойства.
