Тема 6. Средние величины

В результате группировки единиц совокупности по величине варьирующего признака получают ряды распределения – первичную характеристику массовой статистической совокупности. Чтобы охарактеризовать такую совокупность в целом, часто пользуются средней величиной.

Средняя величина – обобщенная количественная характеристика признака статистической совокупности в конкретных условиях места и времени.

Показатель в форме средней величины отражает типичные черты и дает обобщенную характеристику однотипных явлений по одному из варьирующих признаков.

Сущность средней величины заключается в том, что взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием основных факторов.

На практике определить среднюю во многих случаях можно через исходное соотношение средней 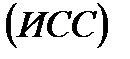или ее логическую формулу:

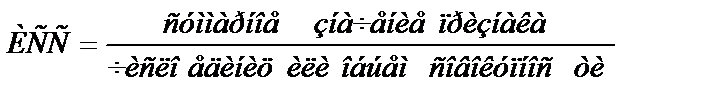(3)

В зависимости от того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение.

Различают следующие виды средней, каждая из которых может быть простой и взвешенной:

– средняя арифметическая;

– средняя гармоническая;

– средняя геометрическая;

– средняя квадратическая;

– структурные средние: мода и медиана.

Средняя арифметическая простая применяется в тех случаях, когда каждое индивидуальное значение признака встречается одинаковое количество раз, то есть когда средняя рассчитывается по группированным единицам совокупности.

Но чаще бывает так, отдельные значения исследуемой совокупности встречается не один, а много, при чем неодинаковое число раз, то есть представляет собой ряд распределения.

В этих случаях рассчитывают среднюю арифметическую взвешенную.

Средняя арифметическая простая. Эта форма средней используется в тех случаях, когда расчет осуществляется по не сгруппированным данным.

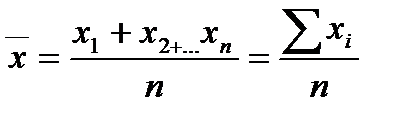(4)

где 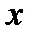– индивидуальные значения признака,

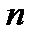– число индивидуальных величин.

Средняя арифметическая взвешенная

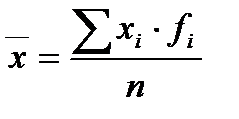(5)

где 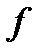– число, показывающее сколько раз повторяются значения признака.

Средняя арифметическая обладает рядом свойств, знания которых необходимо для понимания сущности средних, а также для упрощения их вычисления.

Свойства

1. Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических величин:

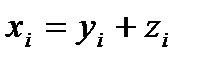(6)

Это правило показывает, в каких случаях можно суммировать средние величины. Если например, выпускаемые изделия состоят из двух деталей y и z и на изготовление каждой из них расходуется в среднем y = 3 ч., z = 5 ч, то средние затраты времени на изготовление одного изделия 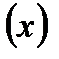, будут равны: 3+5=8ч.

2. Алгебраическая сумма отклонений индивидуальных значений варьирующего признака от средней равна нулю, так сумма отклонений в одну сторону погашается суммой отклонений в другую, то есть .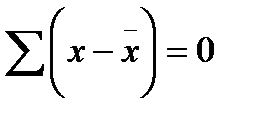

Это правило показывает, что средняя является равнодействующей.

3. Если все варианты ряда уменьшить или увеличить на одно и тоже число 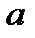, то средняя уменьшится или увеличится на это же число :

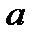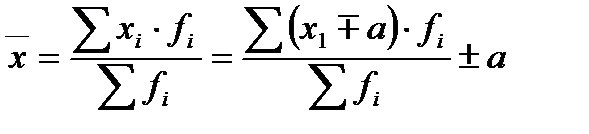(7)

4. Если все варианты уменьшить или увеличить в А раз, то средняя также уменьшится или увеличится в А раз:

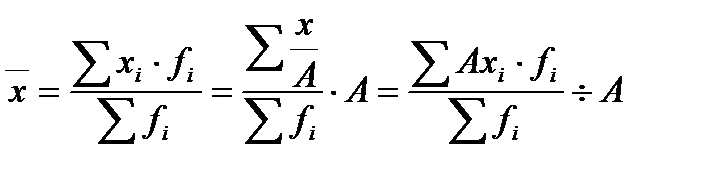(8)

5. Если все частоты ряда разделить или умножить на одно и тоже число d, то средняя не изменится:

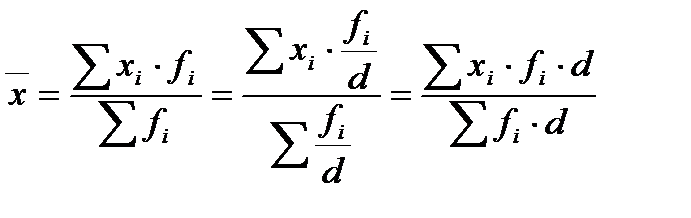(9)

Это свойство показывает, что средняя зависит не от размера весов, а от соотношения между ними. Следовательно, в качестве весов могут выступать не только абсолютные, но и относительные величины.

Другим видом является средняя гармоническая.

Средняя гармоническая – это величина,обратная средней арифметической из обратных значений признака.

Средняя гармоническая простая определяется по формуле:

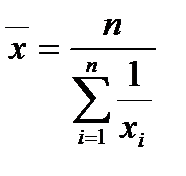(10)

Средняя геометрическая применяется в тех случаях определения средней по значениям, имеющим большой разброс, либо в случаях определения средней величины по относительным показателям:

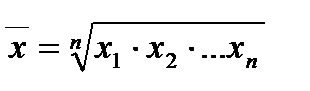(11)

Эту формулу средней геометрической можно сформулировать следующим образом: средняя геометрическая равна корню степени n из произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего.

Средний коэффициент роста можно определить по данным последнего и первого уровней ряда. Если первый уровень ряда обозначить 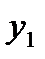, а последний ,

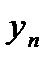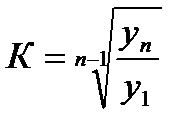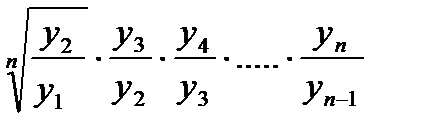или (12)

где n – число лет, а не коэффициентов.

Приведенные формулы идентичны, но одна применяется в тех случаях, когда применяются текущие коэффициенты или темпы роста, а вторая - когда имеются абсолютные значения начального и конечного уровней ряда.

Средняя квадратическая. В тех случаях, когда осреднению подлежат величины, выраженные в виде квадратных функций, применяется средняя квадратическая. Так, средние диаметры колес, труб и др. определяются при помощи средней квадратической.

Средняя квадратическая простая рассчитывается путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число:

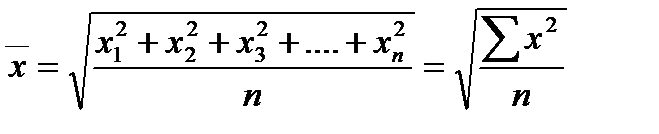(13)

Средняя квадратическая взвешенная равна:

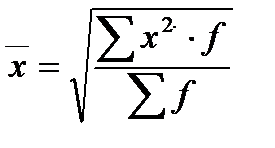(14)

где f – веса.

Степенные средние. Рассмотренные выше средние величины могут быть представлены в форме некоторой системы величин, выделенных из степенной среднего вида:

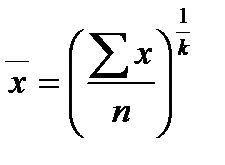(15)

где 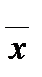– средняя величина;

х – индивидуальные значения признака;

n – число единиц изучаемой совокупности;

к – показатель степени средней.

Придавая показателю степени средней 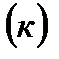различные целые значения, получим отдельные виды степенных средних:

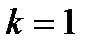– среднюю арифметическую: ;

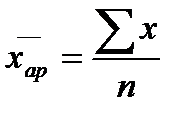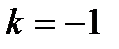– среднюю гармоническую: ;

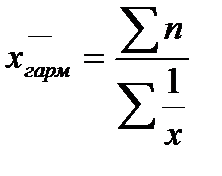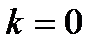– среднюю геометрическую (после преобразований):

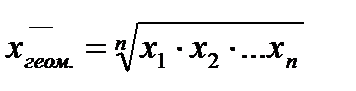(16)

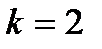– среднюю квадратическую:

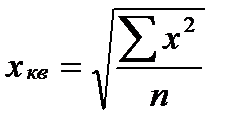. (17)

При расчете различных степенных средних по одним и тем же данным статистических наблюдений средние не будут одинаковы. Чем выше степень k средней, тем больше ее величина.

Математически доказано, что между величинами степенных средних, рассчитанных по одной и тоже совокупности единиц статистического наблюдения и одному и тому же признаку, существует следующее соотношение:

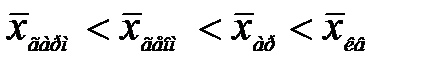(18)

Структурные средние. Для характеристики величины варьирующего признака пользуются так называемыми структурными средними – модой и медианой.

Мода – наиболее часто встречающееся значение ряда. Мода применяется, например, при определении размера одежды, обуви, пользующихся наибольшим спросом у покупателей.

Величина моды и медианы отличается от величины средней, совпадая с ней только в случае симметрии вариационного ряда. При расчете моды для интервального вариационного ряда необходимо сначала определить модальный интервал, в пределах которого находится мода, а затем – значение модальной величины признака. В этом случае моду рассчитывают по следующей формуле:

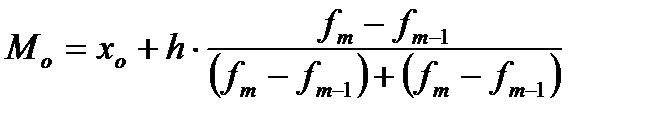(19)

где 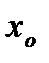– нижняя граница модального интервала;

h – величина модального интервала;

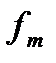– частота интервала, предшествующего модальному;

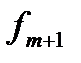– частота интервала, следующего за модальным.

Мода и средняя величина по–разному характеризуют совокупность. Мода по своему обобщающему значению менее точна по сравнению со средней арифметической, характеризующую совокупность в целом с учетом всех без исключения элементов совокупности.

Медианой является значение элемента, который больше или равен, меньше или равен половине остальных элементов ряда распределения. Медиана делит ряд на две равные части.

При нахождении медианы интервального вариационного ряда вначале определяют медианный интервал, в пределах которого находится медиана, а затем приближенное значение медианы по формуле:

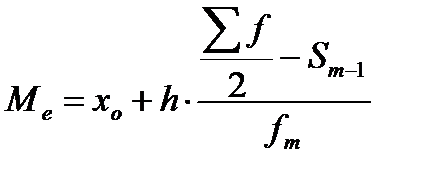(20)

где 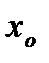– нижняя граница интервала, который содержит медиану;

h - величина медианного интервала;

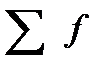– сумма частот;

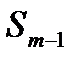– сумма накопленных частот интервалов, предшест-вующих медианному;

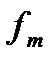– частота медианного интервала.

Медиана не зависит ни от амплитуды колебаний ряда, ни от распределения частот в пределах двух равных частей ряда, поэтому ее применение позволяет получить более точные результаты, чем при использовании других форм средних.

Трудным вопросом методологии является вопрос о выборе вида средней. Здесь необходимо усвоить, что решение этого вопроса зависит от характера исходного соотношения, выражающего среднюю величину, содержания усредняемого признака, его связи с другими признаками, а также от особенностей исходного материала. Каждый из видов средних величин может выступать либо в форме простой, либо взвешенной средней.

Способ определения нужной формы средней, основанный на принципе выяснения сущности средней, ее социально-экономического содержания. Средняя величина признака – это отношение. Поэтому прежде, чем оперировать цифрами, необходимо выяснить, соотношением каких показателей, величин (в конечном счете) является средняя в данном случае.

После того как записана логическая формула средней, которую надо вычислить, необходимо внимательно рассмотреть имеющиеся для вычисления данные и заменить словесные значения числителя и знаменателя логической формулы средней соответствующими числовыми значениями, после чего остается рассчитать только ответ. Этот принцип обеспечит правильный выбор формы средней, а значит правильное определение величины средней.