Тема 9. Индексы

«Индекс» в переводе с латинского – указатель или показатель. В статистике индексом называют показатель относительного изменения данного уровня исследуемого явления по сравнению с другим его уровнем, принятым за базу сравнения. В качестве такой базы может быть использован или уровень за какой-либо прошлый период времени (динамический индекс), или уровень того же явления по другой территории (территориальный индекс). В статистической практике динамические индексы получили большое распространение.

Индексы являются незаменимым инструментом исследования в тех случаях, когда необходимо сравнить во времени или пространстве две совокупности, элементы которых непосредственно суммировать нельзя. Пусть нам необходимо определить рост розничных цен. Здесь уже будет неправомерно складывать цены на разнородные товары, которые могут даже измеряться в различных единицах, а также рассчитывать какие-либо средние показатели. В подобных случаях и применяются индексы.

В целом, индексный метод направлен на решение следующих задач:

1) характеристика общего изменения уровня сложного социально-экономического явления;

2) анализ влияния каждого из факторов на изменение индексируемой величины путём элиминирования воздействия прочих факторов;

3) анализ влияния структурных сдвигов на изменение индексируемой величины.

Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во времени экономических величин, относящихся к одному объекту.

В дальнейшем изложении будут использоваться следующие общепринятые обозначения:

i – индивидуальный индекс;	I – сводный индекс;
p – цена;	z – себестоимость;	q – количество;
r – урожайность;	s – посевная площадь;
(R* s)- валовой сбор,	Е –экономия,	Z*q –затраты на производство,
1 – текущий период;	0 – базисный период.

Рассмотрим индексы:

– индекс цены:

i_p = 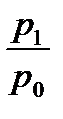, (47)

где р₁ – цена товара в текущем периоде;

р₀ – цена товара в базисном периоде;

– индекс физического объёма реализации:

i_q = 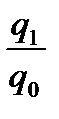, (48)

– индекс товарооборота:

i_pq = 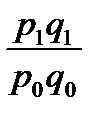. (49)

Индивидуальные индексы в сущности представляют собой относительные показатели динамики или темпы роста, и по данным за несколько периодов времени могут рассчитываться в цепной или базисной формах.

В тех случаях, когда исследуются не единичные объекты, а состоящие из нескольких элементов совокупности, используются сводные индексы. Исходной формой сводного индекса является агрегатная.

При расчёте агрегатного индекса для разнородной совокупности находят такой общий показатель, в котором можно объединить все её элементы. Как уже отмечалось, цены различных товаров складывать неправомерно, но суммировать товарооборот по этим n товарам вполне допустимо. В текущем периоде такой товарооборот составит:

p₁¹q₁¹+p₁²q₁²+p₁³q₁³ +…+ p₁ⁿq₁ⁿ = åp₁q₁ (50)

Аналогично получим для базисного периода:

p₀¹q₀¹ + p₀²q₀² + p₀³q₀³ +…+p₀ⁿq₀ⁿ = åp₀q₀ (51)

Если мы сравним товарооборот в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота:

I_pq = 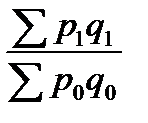. (52)

На величину индекса товарооборота оказывают влияние как изменение цен на товары, так и изменение объёмов их реализации. Для того, чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких показателей, как цена и себестоимость физический объём реализации обычно фиксируют на уровне текущего периода. Таким способом получают сводный индекс цен (по методу Пааше):

I_p = 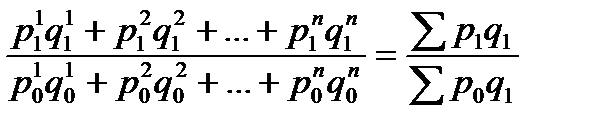. (53)

Числитель данного индекса содержит фактический товарооборот текущего периода. Знаменатель же представляет собой условную величину, показывающую, каким был бы товарооборот в текущем периоде при условии сохранения цен на базисном уровне. Поэтому соотношение этих двух категорий отражает имевшее место изменение цен.

Числитель и знаменатель сводного индекса цен также можно интерпретировать и по-другому. Числитель представляет собой сумму денег, фактически уплаченных покупателями за товары в текущем периоде. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились. Разность числителя и знаменателя будет отражать величину экономии (если знак “-“) или перерасхода («+») покупателей от изменения цен:

Е = åp₁q₁ – åp₀q₁. (54)

Третьим индексом в данной индексной системе является сводный индекс физического объёма продукции. Он характеризует изменение количества проданных товаров не в денежных, а в физических единицах измерения. Весами в данном случае выступают цены, которые фиксируются на базисном уровне:

I_q = 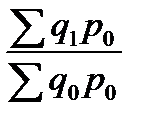. (55)

Между рассчитанными индексами существует следующая взаимосвязь

I_p·I_q = I_pq. (56)

Мы рассмотрели применение индексного метода в анализе товарооборота и цен. Однако эта же индексная система может использоваться для анализа результатов производственной деятельности предприятий, выпускающих разнородную продукцию. Тогда приведённые выше индексы соответственно называются:

I_pq – индекс стоимости продукции;

I_p – индекс оптовых цен;

I_q – индекс физического объёма продукции.

Взаимосвязь между этими индексами остаётся прежней:

I_p·I_q = I_pq. (57)

Ещё одна область применения индексов – анализ затрат на производство.

Индивидуальный индекс себестоимости характеризует изменение себестоимости отдельного вида продукции в текущем периоде по сравнению с базисным.

Для определения общего изменения уровня себестоимости нескольких видов продукции, выпускаемых предприятием, рассчитывается сводный индекс себестоимости. При этом себестоимость взвешивается по объёму производства отдельных видов продукции:

I_z = 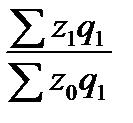. (58)

Числитель этого индекса отражает затраты на производство текущего периода, а знаменатель – условную величину затрат при сохранении себестоимости на базисном уровне. Разность числителя и знаменателя показывает сумму экономии (перерасхода) предприятия от изменения себестоимости:

Е = åz₁q₁ – åz₀q₁. (59)

Индекс физического объёма продукции, взвешенный по себестоимости, имеет следующий вид:

I_q = 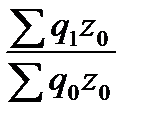. (60)

Третьим показателем в данной индексной системе является индекс затрат на производство:

I_zq = 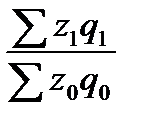. (61)

Все три индекса взаимосвязаны между собой:

I_z*I_q = I_zq. (62)

Индексный метод также находит применение в статистике сельского хозяйства: индекс валового сбора сельскохозяйственных культур (I_rs) может быть получен через индекс урожайности (I_r) и индекс посевных площадей (I_s).

Сводные индексы в средней арифметической и средней гармонической формах

В ряде случаев на практике вместо индексов в агрегатной форме удобнее использовать средние арифметические и средние гармонические индексы. Любой сводный индекс можно представить как среднюю взвешенную из индивидуальных индексов. Однако при этом форму средней нужно выбрать таким образом, чтобы полученный средний индекс был тождественен исходному агрегатному индексу.

Предположим, мы располагаем данными о стоимости проданной продукции в текущем периоде и индивидуальными индексами цен, полученными, например, в результате выборочного наблюдения. Тогда при расчёте сводного индекса цен можно использовать следующую замену:

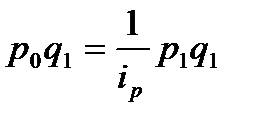. (63)

В целом же сводный индекс цен в данном случае будет выражен в форме средней гармонической:

I_p = 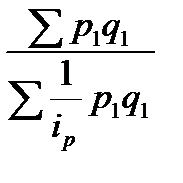. (64)

При расчёте сводного индекса товарооборота можно использовать среднеарифметическую форму. При этом производится замена:

q₁ p₀ = i_q q₀ p₀. (65)

Тогда индекс имеет вид:

I_q = 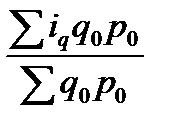. (66)

Индексы могут использоваться для анализа динамики социально-экономических явлений за ряд последовательных периодов. В этом случае для достижения сопоставимости они должны рассчитываться по единой схеме. Такая схема расчёта индексов за несколько временных периодов называется системой индексов.

В зависимости от информационной базы и целей исследователя индексная система может строиться в четырёх вариантах. Рассмотрим их на примере сводного индекса цен, рассчитываемого за n периодов:

А. Цепные индексы цен с переменными весами:

I_p1/0 = 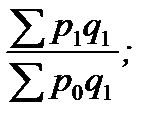I_p2/1 = 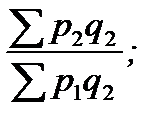… 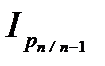= 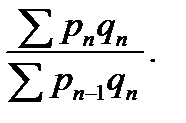(67)

Б. Цепные индексы цен с постоянными весами:

I_p1/0 = 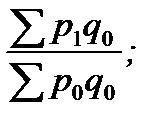I_p2/1 = 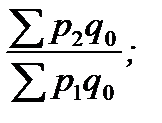…I_pn/n-1 = 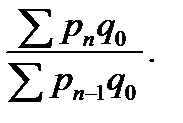(68)

В. Базисные индексы цен с переменными весами:

I_p1/0 = 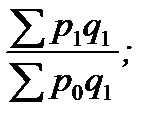I_p2/0 = 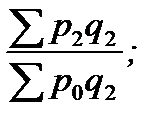…I_pn/0 = 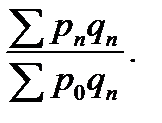(69)

Г. Базисные индексы цен с постоянными весами:

I_p1/0 = 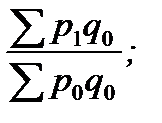I_p2/0 = 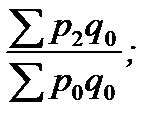…I_pn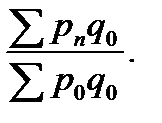/0 = (70)

Индексы переменного и постоянного состава

При анализе отчетных данных изменение количества реализованной продукции (q₁ и q₀ - в индексе физического объема) часто фиксируется по ценам базисного периода p₀, а изменения цен p₁ и p₀ в индексе цен могут фиксироваться по количествам отчетного периода q_1. Такая система фиксации изменений индексируемых величин позволяет их применять в анализе компонентной зависимости:

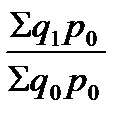х 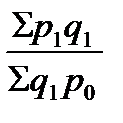= 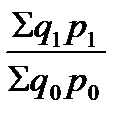. (71)

Взаимосвязанные индексы применяются для изучения влияния структурных сдвигов на изменение социально-экономических явлений. В таком анализе индексы находятся во взаимосвязи со средними величинами. Из формулы средней:

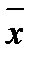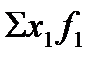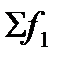= : (72)

следует, что на среднюю величину оказывает влияние как значение осредняемого признака x_i, так и численность отдельных вариантов изучаемой совокупности fi. Так, на среднюю цену овощей, продаваемых на рынках, влияют как различия индивидуальных цен, так и изменения объема реализации. Поэтому при анализе изменения цен важно определить, в какой мере это вызвано изменениями индексируемых величин и в какой - структурными сдвигами количества реализованной продукции. Это выполняется с помощью системы взаимосвязанных индексов, в которой индекс изменения средней величины I 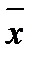выступает как произведение индекса в неизменной структуре I_x на индекс, отображающий влияние изменения структуры явления на динамику средней величины I _стр.

В общем виде эта зависимость записывается так:

I 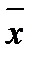= I_x · I _стр.. (73)

При этом:

1) I 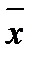= 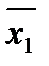: 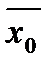= 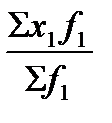: 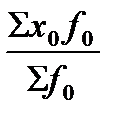. (74)

Индекс (73) называется индексом переменного состава, так как в качестве весов-соизмерителей в нем выступает состав продукции (товаров) текущего fi и базисного fо периодов;

2) I_x = = 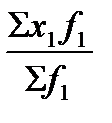: 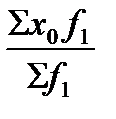= 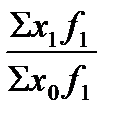. (75)

Индекс (74) называется индексом постоянного (фиксированного) состава, так как в качестве весов-соизмерителей выступает состав продукции (товаров) текущего периода f₁;

3) I _стр = 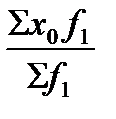: 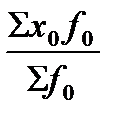. (76)

В индексе (75) изменяются лишь веса-соизмерители f₁ и fо. Поэтому данный индекс отображает влияние структурных сдвигов на изучаемый показатель.